上海市闵行区高三第二次模拟考试数学理
本题共有2个小题,第 1小题满分6分,第2小题满分10分.
1小题满分6分,第2小题满分10分.
某火山喷发停止后,为测量的需要,设距离喷口中心 米内的圆环面为第
米内的圆环面为第 区、
区、 米至
米至 米的圆环面为第
米的圆环面为第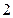 区、……、第
区、……、第 米至
米至 米的圆环面为
米的圆环面为 第
第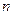 区,…,现测得第
区,…,现测得第 区火山灰平均每平方米为1000千克、第
区火山灰平均每平方米为1000千克、第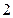 区每平方米的平均重量较第
区每平方米的平均重量较第 区减少
区减少 、第
、第 区较第
区较第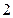 区又减少
区又减少
 ,以此类推,求:
,以此类推,求:
(1)离火山口1225米处的圆环面平均每平方米火山灰重量(结果精确到1千克)?
(2)第几区内的火 山灰总重量最大?
山灰总重量最大?
本题共有3个小题 ,第1小题满分4分,第2小题满分6分、第3小题满分6分.
,第1小题满分4分,第2小题满分6分、第3小题满分6分.
设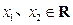 ,常数
,常数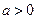 ,定义运算“
,定义运算“ ”:
”: ,定义运算“
,定义运算“ ”:
”: ;对于两点
;对于两点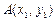 、
、 ,定义
,定义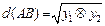 .
.
(1)若 ,求动点
,求动点 的轨迹
的轨迹 ;
;
(2)已知直线 与(1)中轨迹
与(1)中轨迹 交于
交于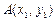 、
、 两点,若
两点,若 ,试求
,试求
 的值;
的值;
(3)在(2)中条件下,若直线 不过原点且与
不过原点且与 轴交于点S,与
轴交于点S,与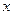 轴交于点T,并且与(1)中轨迹
轴交于点T,并且与(1)中轨迹 交于不同两点P、Q , 试求
交于不同两点P、Q , 试求 的取值范围.
的取值范围.
 (
( 为虚数单位,
为虚数单位, ),则
),则 .
. 、
、 是两个随机事件,
是两个随机事件, ,
, ,
, ,则
,则 .
. 的
的 解为 .
解为 . 展开式中
展开式中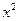 的系数为
的系数为 
 .
.
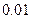 ).
).
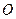 的半径为
的半径为 ,一平面截球所得的截面面积为
,一平面截球所得的截面面积为 ,球心
,球心 ,则球
,则球
 的零点
的零点 ,
, .
. 的前
的前 项之和
项之和 满足
满足 ,
, .
.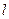 的参数方程是
的参数方程是 (
( 是参数),以原点
是参数),以原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 ,则圆
,则圆 的距离是 .
的距离是 . 的两个不等式
的两个不等式 和
和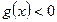 的解集分别为
的解集分别为 和
和 ,则称这两个不等式为对偶不等式.如果不等式
,则称这两个不等式为对偶不等式.如果不等式 与不等式
与不等式 为对偶不等式,且
为对偶不等式,且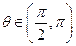 ,则
,则 .
. 是方程
是方程 (
( 是实常数)
是实常数) 的一个根,
的一个根, 是
是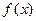 的反函数,则方程
的反函数,则方程 必有一根是 .
必有一根是 . 在
在 上是增函数的一个充分非必要条件是 .
上是增函数的一个充分非必要条件是 . 自然数
自然数
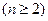 的正整数次幂,可以如下分解为
的正整数次幂,可以如下分解为


 的分解中的最大数为 .
的分解中的最大数为 .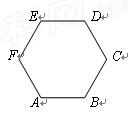
 .
. .
. .
. .
. 中,
中, ,
,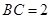 ,则角
,则角 的取值范围是 ( )
的取值范围是 ( ) .
. .
. .
. .
.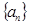 中,已知
中,已知 ,
, ,
, ,若对任意正整数
,若对任意正整数 ,有
,有 ,且
,且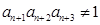 ,则该数列的前2010 项和
,则该数列的前2010 项和 ( )
( ) .
. .
. .
.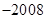 .
. 是曲线
是曲线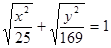 上的点,又点
上的点,又点 ,下列结
,下列结 .
. .
.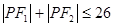 .
. .
. ,
,  .
. ,求函数
,求函数 的值;
的值;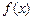 的值域.
的值域. 中,底面为直角梯形,
中,底面为直角梯形, ,
, 垂直于底面
垂直于底面 ,
, ,
,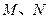 分别为
分别为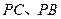 的中点.
的中点.  ;
; 与平面
与平面 所成的角.
所成的角.
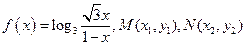 是
是 图像上的两点,横坐标为
图像上的两点,横坐标为 的点
的点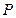 满足
满足 (
( 为坐标原点).
为坐标原点). 为定值;
为定值;
 ,
,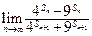 的
的 值;
值;
 ,
, 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切 都成立,试求实数
都成立,试求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号