河南省驻马店高中2010届高三一模(数学文)
设 与
与 是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],都有
是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],都有 成立,则称
成立,则称 和
和 在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若
在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若 与
与 在[a,b]上是“密切函数”,则其“密切区间”可以是( )
在[a,b]上是“密切函数”,则其“密切区间”可以是( )
| A.[1,4] | B.[2,4] | C.[3,4] | D.[2,3] |
已知定义在R上的函数 满足条件
满足条件 ,且函数
,且函数 是奇函数,给出以下四个命题:
是奇函数,给出以下四个命题:
①函数 是周期函数;
是周期函数;
②函数 的图象关于点
的图象关于点 对称;
对称;
③函数 是偶函数;
是偶函数;
④函数在R上是单调函数。
在上述四个命题中,真命题的序号是 (写出所有的真命题的序号)。
)已知向量 =(sin(
=(sin( +x),
+x), cosx),
cosx), =(sinx,cosx), f(x)=
=(sinx,cosx), f(x)=  ·
· .
.
⑴求f(x)的最小正周期和单调增区间;
⑵如果三角形ABC中,满足f(A)= ,求角A的值.
,求角A的值.
某隧道长2150米,通过隧道的车速不能超过20米/秒.一个由55辆车身都为10米的同一车型组成的运输车队匀速通过该隧道.设车队的速度为x米/秒,根据安全和车流的需要,相邻两车均保持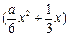 米的距离,其中a为常数且
米的距离,其中a为常数且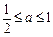 ,自第一辆车车头进入隧道至第55辆车车尾离开隧道所用时间为y(秒) .
,自第一辆车车头进入隧道至第55辆车车尾离开隧道所用时间为y(秒) .
(1)将y表示为x的函数;
(2)求车队通过隧道所用时间取最小值时车队的速度.
 ( )
( ) 过点
过点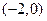 ,当直线
,当直线 有两个交点时,其斜率
有两个交点时,其斜率 的取值范围是( )
的取值范围是( )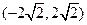
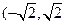 )
)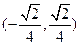

 ,条件
,条件 ,则
,则 是
是 的( )
的( ) 是两个向量集合,则
是两个向量集合,则 ( )
( ) (x∈R,
(x∈R, )的图像的最高点,M、N是图像与
)的图像的最高点,M、N是图像与 轴的交点,
轴的交点, ,则
,则




 展开式中各项二项式系数之和为
展开式中各项二项式系数之和为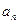 ,
, 展开式中各项系数之和为
展开式中各项系数之和为 ,则
,则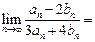 ( )
( )

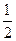

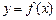 是圆心在原点的单位圆的两段圆弧,则不等式
是圆心在原点的单位圆的两段圆弧,则不等式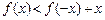 的解集为( )
的解集为( )
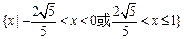

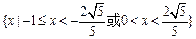
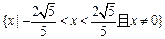
 ,则
,则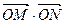 的最大值是( )
的最大值是( ) 的前n项和为
的前n项和为 ,且
,且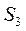 =6,
=6,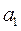 =4,则公差d等于( )
=4,则公差d等于( ) C.- 2 D 3
C.- 2 D 3 是R上的连续偶函数,且当
是R上的连续偶函数,且当 时
时 的所有
的所有 之和为( )
之和为( ) (p>0)与双曲线
(p>0)与双曲线 (a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率
(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率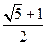 B
B  C
C 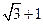 D
D 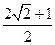
 。
。 的解集是_______________。
的解集是_______________。 上的函数
上的函数 满足
满足 ,若
,若 ,则
,则
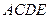 所在的平面与平面
所在的平面与平面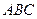 垂直,
垂直,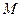 是
是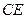 和
和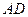 的交点,
的交点,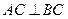 ,且
,且 .
.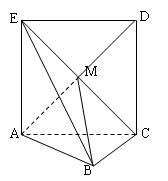
 平面
平面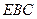 ;
; 与平面
与平面 的大小.
的大小. ,
, .
. 的单调区间;
的单调区间; 内是减函数,求
内是减函数,求 的取值范围.
的取值范围. ,且
,且 (
(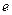 为自然对数的底数).
为自然对数的底数).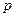 与
与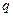 的关系;
的关系;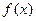 在其定义域内为单调函数,求实数
在其定义域内为单调函数,求实数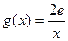 ,若存在
,若存在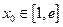 ,使得
,使得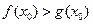 成立,求实数
成立,求实数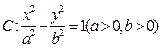 的离心率为
的离心率为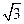 ,右准线方程为
,右准线方程为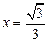
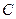 的方程;
的方程;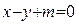 与双曲线C 交于不同的两点A,B,且线段AB的中点在圆
与双曲线C 交于不同的两点A,B,且线段AB的中点在圆 上,求m的值.
上,求m的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号