[贵州]2013届贵州省六校联盟高三第一次联考理科数学试卷
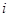 是虚数单位,则复数
是虚数单位,则复数 在复平面内对应的点在( )
在复平面内对应的点在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
投掷一枚质地均匀的骰子两次,若第一次面向上的点数小于第二次面向上的点数我们称其为前效实验,若第二次面向上的点数小于第一次面向上的点数我们称其为后效实验,若两次面向上的点数相等我们称其为等效试验.那么一个人投掷该骰子两次后出现等效实验的概率是( )
A. |
B. |
C. |
D. |
设曲线 与抛物线
与抛物线 的准线围成的三角形区域(包含边界)为
的准线围成的三角形区域(包含边界)为 ,
, 为
为 内的一个动点,则目标函数
内的一个动点,则目标函数 的最大值为( )
的最大值为( )
A. |
B. |
C. |
D. |
某几何体的三视图如图所示,图中的四边形都是边长为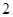 的正方形,两条虚线互相垂直,则该几何体的体积是( )
的正方形,两条虚线互相垂直,则该几何体的体积是( )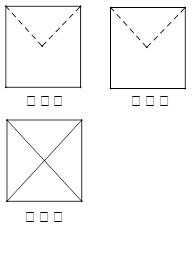
A. |
B.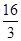 |
C. |
D.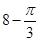 |
给出下列四个命题:
(1)命题“若 ,则
,则 ”的逆否命题为假命题;
”的逆否命题为假命题;
(2)命题 .则
.则 ,使
,使 ;
;
(3)“ ”是“函数
”是“函数 为偶函数”的充要条件;
为偶函数”的充要条件;
(4)命题 “
“ ,使
,使 ”;命题
”;命题 “若
“若 ,则
,则 ”,那么
”,那么 为真命题.其中正确的个数是( )
为真命题.其中正确的个数是( )
A. |
B. |
C. |
D. |
已知函数 的图象如图所示(其中
的图象如图所示(其中 是函数
是函数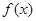 的导函数).下面四个图象中,
的导函数).下面四个图象中,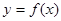 的图象大致是( )
的图象大致是( )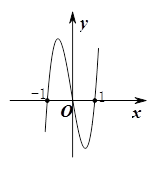
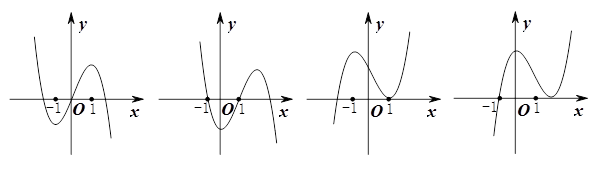
| A. |
B. |
C. |
D. |
我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知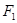 、
、 是一对相关曲线的焦点,
是一对相关曲线的焦点,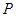 是它们在第一象限的交点,当
是它们在第一象限的交点,当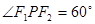 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( )
A.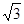 |
B.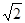 |
C.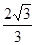 |
D. |
正方体 的棱长为
的棱长为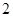 ,
, 是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦),
是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦), 为正方体表面上的动点,当弦
为正方体表面上的动点,当弦 的长度最大时,
的长度最大时,

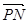 的取值范围是 .
的取值范围是 .
(本小题满分12分)已知 ,
, ,且
,且 .
.
(I)将 表示成
表示成 的函数
的函数 ,并求
,并求 的最小正周期;
的最小正周期;
(II)记 的最大值为
的最大值为 ,
, 、
、 、
、 分别为
分别为 的三个内角
的三个内角 、
、 、
、 对应的边长,若
对应的边长,若 且
且 ,求
,求 的最大值.
的最大值.
(本小题满分12分)为了参加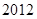 年贵州省高中篮球比赛,某中学决定从四个篮球较强的班级中选出
年贵州省高中篮球比赛,某中学决定从四个篮球较强的班级中选出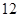 人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
| 班级 |
高三( )班 )班 |
高三(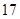 )班 )班 |
高二(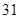 )班 )班 |
高二(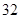 )班 )班 |
| 人数 |
 |
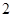 |
 |
 |
(I)从这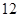 名队员中随机选出两名,求两人来自同一班级的概率;(II)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为
名队员中随机选出两名,求两人来自同一班级的概率;(II)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为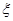 ,求随机变量
,求随机变量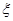 的分布列及数学期望
的分布列及数学期望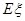 .
.
(本小题满分12分)如图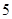 ,已知在四棱锥
,已知在四棱锥 中,底面
中,底面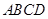 是矩形,
是矩形, 平面
平面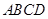 ,
, ,
, ,
, 是
是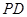 的中点,
的中点,  是线段
是线段 上的点.
上的点.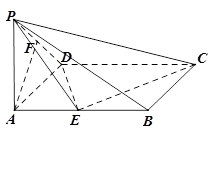
(I)当 是
是 的中点时,求证:
的中点时,求证: 平面
平面 ;
;
(II)要使二面角 的大小为
的大小为 ,试确定
,试确定 点的位置.
点的位置.
(本小题满分12分)
已知椭圆 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点 .
.
(I)求椭圆 的方程;
的方程;
(II)直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点,  为原点,在
为原点,在 、
、 上分别存在异于
上分别存在异于 点的点
点的点 、
、 ,使得
,使得 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 在点
在点 处的切线方程为
处的切线方程为 .
.
(I)求 ,
, 的值;
的值;
(II)对函数 定义域内的任一个实数
定义域内的任一个实数 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 ,
, ,则
,则 等于( )
等于( )



 的前
的前 项和为
项和为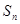 ,已知
,已知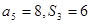 ,则
,则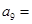 ( )
( )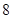

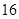

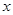 的值为
的值为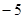 ,则输出的
,则输出的 值是( )
值是( )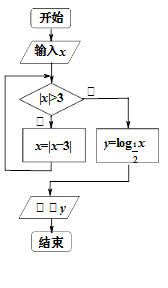
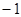
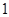

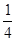
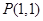 为圆
为圆 的弦
的弦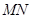 的中点,则弦
的中点,则弦


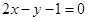
 ,
, ,
, ,则( )
,则( )



 科成绩如茎叶图
科成绩如茎叶图 所示,则根据茎叶图可知该同学的平均分为 .[
所示,则根据茎叶图可知该同学的平均分为 .[
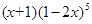 展开式中,
展开式中,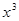 的系数为 (用数字作答).
的系数为 (用数字作答). 中,
中,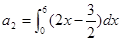 ,
,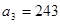 ,若数列
,若数列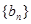 满足
满足 ,则数列
,则数列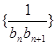 的前
的前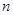 项和
项和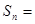 .
.
 的图象;
的图象; 的不等式
的不等式 有解,求实数
有解,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号