广东省中山市初一上学期期末数学卷
下列事件是随机事件的是( ▲ ).
| A.在一个标准大气压下,加热到100℃,水沸腾 |
| B.购买一张福利彩票,中奖 |
| C.有一名运动员奔跑的速度是30米/秒 |
| D.在一个仅装着白球和黑球的袋中摸球,摸出红球 |
如图所示,已知点E、F分别是△ABC中AC、AB边的中点,BE、CF相交于点G,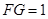 ,则CF的长为( ).
,则CF的长为( ). 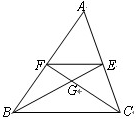
A.2
B.1.5
C.3
D.4
把抛物线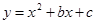 的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为
的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为 ,则
,则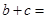 ( ▲ ).
( ▲ ).
| A.12 | B.9 | C.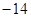 |
D.10 |
如图,△ABC是直角边长为4的等腰直角三角形,直角边AB是半圆O1的直径,半圆O2过C点且与半圆O1相切,则图中阴影部分的面积是( )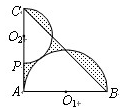
A.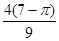 |
B.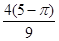 |
C. |
D. |
如图,在平行四边形ABCD中,点E在边BC上,BE:EC=1:2,连接AE交BD于点F,则△BEF的面积与△ADF的面积之比为 ▲ .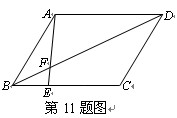
将直角边长为3cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△ADE,则图中阴影部分的面积为 ▲ cm2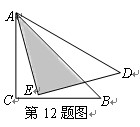
如图所示,AB为⊙O的直径,P点为其半圆上一点,∠POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB= ▲ 度.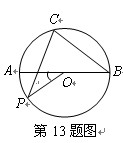
一个密码箱的密码, 每个数位上的数都是从0到9的自然数,若要使不知道密码的人一次就拨对密码的概率小于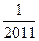 ,则密码的位数至少需要 ▲ 位
,则密码的位数至少需要 ▲ 位
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C, 交半圆于点F.已知BD=2,设AD=x,CF=y,则y关于x的函数解析式是 ▲ .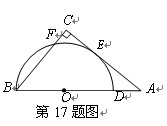
如图,在Rt△ABC中,∠A=90°,AB=AC=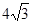 ,点D为AC的中点,点E在边BC 上,且ED⊥BD,则△CDE的面积是 ▲ .
,点D为AC的中点,点E在边BC 上,且ED⊥BD,则△CDE的面积是 ▲ .
(本小题8分)
关于x的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围.
(2)请选择一个k的负整数值,并求出方程的根
(本小题10分)
抛物线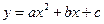 经过点O(0,0),A(4,0),B(2,2).
经过点O(0,0),A(4,0),B(2,2).
(1)求该抛物线的解析式;
(2)画出此抛物线的草图;
(3)求证:△AOB是等腰直角三角形;
(4)将△AOB绕点O按顺时针方向旋转135°得△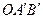 ,写出边
,写出边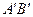 的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
“把弯曲的公路改直,就能缩短路程”,其中蕴含的数学道理是 ( )
| A.两点确定一条直线 | B.直线比曲线短 |
| C.两点之间直线最短 | D.两点之间线段最短 |
如图,已知O是直线AD上的点, 三个角∠AOB、∠BOC、∠COD从小到大依次相差20度, 则∠AOB= 度.
如图, 一艘客轮沿东北方向OC行驶,在海上O处发现灯塔A在北偏西30°方向上, 灯塔B在南偏东60°方向上.
(1)在图中画出射线OA、OB、OC;
(2)求∠AOC与∠BOC的度数,你发现了什么?
用同样规格的黑白两种颜色的正方形,按如图的方式拼图,请根据图中的信息完成下列的问题.
(1)在图②中用了 块黑色正方形,在图③中用了 块黑色正方形;
(2)按如图的规律继续铺下去,那么第 个图形要用 块黑色正方形;
个图形要用 块黑色正方形;
(3)如果有足够多的白色正方形,能不能恰好用完90块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
 有意义,a的取值范围是( ▲ ).
有意义,a的取值范围是( ▲ ).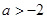
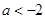
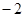

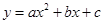 的图像如图所示,当函数值
的图像如图所示,当函数值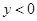 时,x的取值范围为
时,x的取值范围为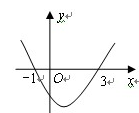
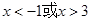

 x≥3
x≥3 ≤x≤3
≤x≤3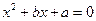 有一个根是
有一个根是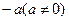 ,则下列代数式的值恒为常数的是( ▲ ).
,则下列代数式的值恒为常数的是( ▲ ).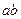
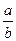
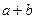
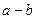
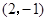 关于原点对称的点B的坐标为 ▲
关于原点对称的点B的坐标为 ▲ 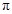 ).
).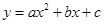 的图象如图,则下列5个代数式:①ac,②
的图象如图,则下列5个代数式:①ac,②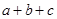 ,③
,③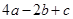 ,④
,④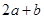 ,⑤
,⑤ ,⑥
,⑥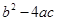 中,其值大于0的序号为 ▲
中,其值大于0的序号为 ▲ 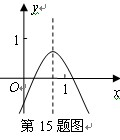
 的两个实数根,那么
的两个实数根,那么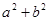 的最小值是 ▲ .
的最小值是 ▲ .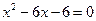
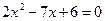 (用配方法解)
(用配方法解)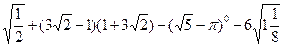
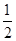
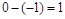
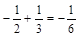
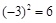
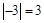
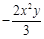 的系数是
的系数是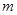 ,次数是
,次数是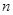 ,则
,则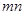 的值为 ( )
的值为 ( )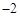
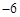
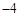
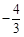
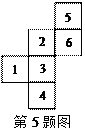
 ,将5 280 000用科学记数法表示为
,将5 280 000用科学记数法表示为  、
、 、
、 、
、 的四张卡片中抽出两张卡片,使其能合并同类项,则抽出的卡片分别标有 、 .
的四张卡片中抽出两张卡片,使其能合并同类项,则抽出的卡片分别标有 、 .


 ,4
,4


 ,
, ,且
,且 ,求
,求 的值
的值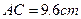 ,
,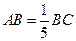 ,
, ,求
,求 的长
的长
 粤公网安备 44130202000953号
粤公网安备 44130202000953号