[福建]2011-2012学年福建邵武市邵中片七年级下学期期中测试数学试卷
点P的坐标是(4,-3),则点P所在象限是 ( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
下列长度的三条线段可以组成三角形的是 ( )
| A.1,2,3 | B.3,4,5 | C.2,3,6 | D.2,2,7 |
已知:如图,OC⊥AB,DE平分∠AOC,那么∠AOE等于 ( )
| A.135° | B.50° | C.45° | D.155° |

如图,直线l1∥l2,∠1=55°,则∠2为 ( )
| A.35° | B.45° | C.55° | D.125° |

一个正多边形的每个内角都是144°,那么这个正多边形的内角和是 ( )
| A.14400 | B.12600 | C.10800 | D.9000 |
小亮的父亲想购买同一种大小一样、形状相同的地板铺设地面,小亮根据所学知识告诉父亲,
为了能够做到无缝、不重叠地铺设,购买的地板砖形状不能是 ( )
| A.正三角形 | B.正方形 | C.正五边形 | D.正六边形 |
下列命题中,假命题是 ( )
| A.在同一平面内,如果a⊥b,b⊥c,那么a//c |
| B.如果a//b,b//c,那么a//c |
| C.相等的两个角是对顶角 |
| D.如果一个角等于120°,那么它的补角是60° |
如图,下列推理及所注明的理由都正确的是: ( )
| A.因为DE∥BC,所以∠1=∠C(同位角相等,两直线平行) |
| B.因为∠2=∠3,所以DE∥BC(两直线平行,内错角相等) |
| C.因为∠1=∠C,所以DE∥BC(两直线平行,同位角相等) |
| D.因为DE∥BC,所以∠2=∠3(两直线平行,内错角相等) |

如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠BOC=120°,则∠A的度数为 ( )
| A.40° | B.50° | C.60° | D.120° |

如图,直线AB、CD相交于O,且∠AOD=50°,则∠BOC的度数为________.
课间操时,小华、小军、小刚的位置如图7,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成___________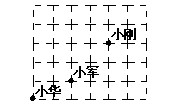
如图,用吸管吸易拉罐内的饮料时,∠1=110°,则∠2= (易拉罐的上下底面互相平行)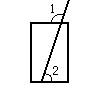
如图,Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=35°,则∠A的度数为________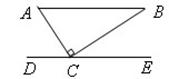
把命题“垂直于同一条直线的两条直线互相平行”改写成“如果…,那么…”的形式为________.
如图,小明在操场上从A点出发,沿直线前进10米后向左转40o,再沿直线前进10米后,又向左转40o,……,照这样走下去,他第一次回到出发地A点时,一共走了 米.
△ABC在如图所示的平面直角坐标系中, 将其平移后得△A′B′C′, 若B的对应点B’的坐标是(4,1).
①在图中画出△A′B′C′;
② 此次平移可看作将△ABC向_____平移了_____个单位长度, 再向_____平移了_____个单位长度得△A′B′C′;
③△A’B’C’的面积为____________. 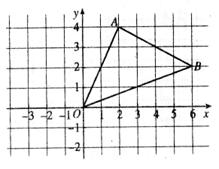
已知:如图,△ABC,请在图中作出①AB边上的中线CD,②∠BAC的平分线AE,③BC边上的高AF.
这是一个动物园游览示意图,试建立一个适当的平面直角坐标系描述这个动物园图中每个景点位置,(画出图形,并写出各景点的坐标)。 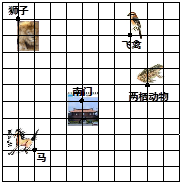
根据提示填空(或填上每步推理的理由)
如图,∠1=∠2,∠3=108°.求∠4的度数。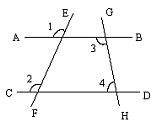
解:∵∠1=∠2(已知)
∴AB∥CD( )
∴∠3+∠4=180°( )
∵∠3=108°(已知)
∴∠4=180°-108°=72°
根据提示填空(或填上每步推理的理由)
已知:如图,∠1=∠2、∠3=∠4,求证:∠5=∠A.
证明:∵∠1=∠2.(已知)
∠3=∠4,(已知)
又∵∠2=∠3( )
∴∠1=∠4.( )
∴_______//_______( )
∴∠5=∠A( )
如图,AB∥CD,EF分别交AB、CD于M、N ∠EMB=50°,MG平分∠BMF,MG交CD于G.求∠1的度数. 
如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=66°,∠ACB=74°,∠AED=48°,求∠BDF, ∠F的度数
如图,AF是△ABC的高,AD是△ABC的角平分线,且∠B=38°,∠C=72°,求∠DAF的度数.

 是方程2x+ay=5的解,则a = 。
是方程2x+ay=5的解,则a = 。





 粤公网安备 44130202000953号
粤公网安备 44130202000953号