[四川]2012年初中毕业升学考试(四川乐山卷)数学
如果规定收入为正,支出为负.收入500 元记作500元,那么支出237元应记作【 】
| A.﹣500元 | B.﹣237元 | C.237元 | D.500元 |
下列命题是假命题的是【 】
| A.平行四边形的对边相等 | B.四条边都相等的四边形是菱形 |
| C.矩形的两条对角线互相垂直 | D.等腰梯形的两条对角线相等 |
⊙O1的半径为3厘米,⊙O2的半径为2厘米,圆心距O1O2=5厘米,这两圆的位置关系是【 】
| A.内含 | B.内切 | C.相交 | D.外切 |
如图,A、B两点在数轴上表示的数分别为a、b,下列式子成立的是【 】
A.ab>0 B.a+b<0 C.(b﹣1)(a+1)>0 D.(b﹣1)(a﹣1)>0
若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是【 】
A. |
B. |
C. |
D. |
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 .
.
其中正确结论的个数是【 】
A.1个 B.2个 C.3个 D.4个
二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(﹣1,0).设t=a+b+1,则t值的变化范围是【 】
| A.0<t<1 | B.0<t<2 | C.1<t<2 | D.﹣1<t<1 |
从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
如图,⊙O是四边形ABCD的内切圆,E、F、G、H是切点,点P是优弧 上异于E、H的点.若∠A=50°,则∠EPH= .
上异于E、H的点.若∠A=50°,则∠EPH= .
一个盒中装着大小、外形一模一样的x颗白色弹珠和y颗黑色弹珠,从盒中随机取出一颗弹珠,取得白色弹珠的概率是 .如果再往盒中放进12颗同样的白色弹珠,取得白色弹珠的概率是
.如果再往盒中放进12颗同样的白色弹珠,取得白色弹珠的概率是 ,则原来盒中有白色弹珠 颗.
,则原来盒中有白色弹珠 颗.
如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An.设∠A= .则:
.则:
(1)∠A1= ;(2)∠An= .
如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.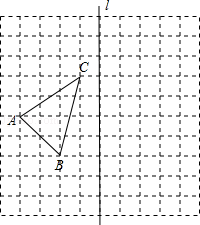
在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的单价对外批发销售.
(1)求平均每次下调的百分率;
(2)小华准备到李伟处购买5吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金200元.
试问小华选择哪种方案更优惠,请说明理由.
如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据: ,
, )
)
已知关于x的一元二次方程(x﹣m)2+6x=4m﹣3有实数根.
(1)求m的取值范围;
(2)设方程的两实根分别为x1与x2,求代数式x1•x2﹣x12﹣x22的最大值.
如图,直线y=2x+2与y轴交于A点,与反比例函数 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数 (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF;
②当AB=4,AD= 时,求线段BG的长.
时,求线段BG的长.
如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.









 |= .
|= . ,并求出它的整数解的和.
,并求出它的整数解的和.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号