2010年高级中等学校招生全国统一考试数学卷(海南)
如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP长不可能是(▲)
| A.2.5 | B.3 | C.4 | D.5 |
如图,⊙O的直径CD⊥AB,∠AOC=50°,则∠CDB大小为 (▲)
| A.25° | B.30° | C.40° | D.50° |
下列说法中正确的是(▲)
| A.“打开电视,正在播放《新闻联播》”是必然事件; |
B.某次抽奖活动中奖的概率为 ,说明每买100张奖券,一定有一次中奖; ,说明每买100张奖券,一定有一次中奖; |
| C.数据1,1,2,2,3的众数是3; |
| D.想了解台州市城镇居民人均年收入水平,宜采用抽样调查. |
梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,则下底BC的长是(▲)
| A.3 | B.4 | C.2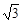 |
D.2+2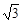 |
如图,矩形ABCD中,AB>AD,AB=a,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N.则DM+CN的值为(用含a的代数式表示)(▲)
| A.a | B. |
C. |
D. |
如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为
的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为 ,则点D的横坐标最大值为(▲)
,则点D的横坐标最大值为(▲)
A.-3 B.1 C.5 D.8
某种商品原价是120元,经两次降价后的价格是100元,求平均每次降价的百分率.设平均每次降价的百分率为 ,可列方程为 ▲ .
,可列方程为 ▲ .
如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图,
观察图形,甲、乙这10次射击成绩的方差 ,
, 之间的大小关系是 ▲ .
之间的大小关系是 ▲ .
如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于E.
则直线CD与⊙O的位置关系是 ▲ ,阴影部分面积为(结果保留π) ▲ .
如图,菱形ABCD中,AB="2" ,∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O所经过的路径总长为(结果保留π) ▲ .
施工队准备在一段斜坡上铺上台阶方便通行.现测得斜坡上铅垂的两
棵树间水平距离AB=4米,斜面距离BC=4.25米,斜坡总长DE=85米.
(1)求坡角∠D的度数(结果精确到1°);
(2)若这段斜坡用厚度为17cm的长方体台阶来铺,需要铺几级台阶?
A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶7了小时时,两车相遇,求乙车速度.
果农老张进行杨梅科学管理试验.把一片杨梅林分成甲、乙两部分,甲地块用新技术管理,乙地块用老方法管理,管理成本相同.在甲、乙两地块上各随机选取20棵杨梅树,根据每棵树产量把杨梅树划分成A,B,C,D,E五个等级(甲、乙的等级划分标准相同,每组数据包括左端点不包括右端点).画出统计图如下:
(1)补齐直方图,求 的值及相应扇形的圆心角度数;
的值及相应扇形的圆心角度数;
(2)选择合适的统计量,比较甲乙两地块的产量水平,并说明试验结果;
(3)若在甲地块随机抽查1棵杨梅树,求该杨梅树产量等级是B的概率.
类比学习:
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+( )=1.
)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 .
.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1) 观察:
①如图2、图3,当∠CDF="0°" 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF="30°" 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果 ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和 的值.
的值.
如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
(3)当x为何值时,△HDE为等腰三角形?
同一平面内,半径分别是2cm和3cm的两圆的圆心距为5cm,则这两圆的位置关系是
| A.相离 | B.相交 | C.外切 | D.内切 |
如图4, 在梯形ABCD中,AD//BC,AC与BD相交于点O,则下列三角形中,与△BOC一定相似的是
| A.△ABD | B.△DOA | C.△ACD | D.△ABO |
如图5, 在△ABC中,AB=AC,AD⊥BC于点D,则下列结论不一定成立的是
| A. | B.BD = CD | C. 1 = 1 = 2 2 |
D. B = B = C C |
海南省农村公路通畅工程建设,截止2009年9月30日,累计完成投资约4 620 000 000元,数据4 620 000 000用科学记数法表示应为____________.
一道选择题共有四个备选答案,其中只有一个是正确的,若有一位同学随意选了其中一个答案,那么他选中正确答案的概率是_________.
如图6,在平行四边形ABCD中,AB = 6cm,∠BCD的平分线交AD于点 ,则线段DE的长度是__________ cm.
,则线段DE的长度是__________ cm.
如图7,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB的长度为_________cm.
(满分8分)
从相关部门获悉,2010年海南省高考报名人数共54741人,图8是报名考生分类统计图
根据以上信息,解答下列问题:
(1)2010年海南省高考报名人数中,理工类考生___________人;
(2)请补充完整图8中的条形统计图和扇形统计图(百分率精确到0.1%);
(3)假如你自己绘制图8中扇形统计图,你认为文史类考生对应的扇形圆心角应为 °(精确到1°).
(满分8分)如图9,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向右平移5个单位长度,画出平移后的△A1B1C1 ;
(2)画出△ABC关于x轴对称的△A2B2C2 ;
(3)将△ABC绕原点O 旋转180°,画出旋转后的△A3B3C3 ;
(4)在△A1B1C1 、△A2B2C2 、△A3B3C3 中△________与△________成轴对称;△________与△________成中心对称.
(满分8分)
2010年上海世博会入园门票有11种之多,其中“指定日普通票”价格为200元一张,“指定日优惠票”价格为120元一张,某门票销售点在5月1日开幕式这一天共售出这两种门票1200张,收入216000元,该销售点这天分别售出这两种门票多少张?
(满分11分)
如图,四边形ABCD和四边形AEFG均为正方形,连接BG与DE相交于点H.
(1)证明:△ABG 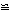 △ADE ;
△ADE ;
(2)试猜想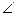 BHD的度数,并说明理由;
BHD的度数,并说明理由;
(3)将图中正方形ABCD绕点A逆时针旋转(0°<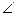 BAE <180°),设△ABE的面积为
BAE <180°),设△ABE的面积为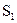 ,△ADG的面积为
,△ADG的面积为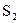 ,判断
,判断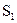 与
与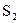 的大小关系,并给予证明.
的大小关系,并给予证明.
 的绝对值是(▲)
的绝对值是(▲)



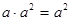
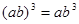
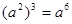

 图象上有三个点
图象上有三个点 ,
, ,
, ,其中
,其中 ,则
,则 ,
, ,
, 的大小关系是(▲)
的大小关系是(▲)



 的自变量
的自变量 的取值范围是 ▲ .
的取值范围是 ▲ . = ▲ .
= ▲ . ;
;  .
.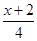 ≤
≤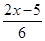 ,并把解集在数轴上表示出来
,并把解集在数轴上表示出来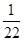
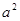

 有意义,则
有意义,则 的取值范围是
的取值范围是

 、
、 、
、 分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是
分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是



 的位置如图3所示,则
的位置如图3所示,则  的值是
的值是



 的图象的任一支上,
的图象的任一支上, 都随
都随 的增大而增大,则
的增大而增大,则 的值可以是
的值可以是 __________.
__________. 天生产60件产品,则平均每天生产该产品__________件.
天生产60件产品,则平均每天生产该产品__________件. (2)解方程:
(2)解方程:
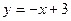 与
与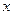 轴、
轴、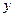 轴分别交于点B、C ;抛物线
轴分别交于点B、C ;抛物线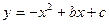 经过B、C两点,并与
经过B、C两点,并与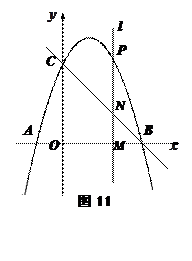
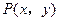 是(1)所得抛物线上的一个动点,过点P作直线
是(1)所得抛物线上的一个动点,过点P作直线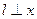 轴于点M,交直线BC于点N .
轴于点M,交直线BC于点N . 粤公网安备 44130202000953号
粤公网安备 44130202000953号