[北京]2012届北京石景山中考二模数学试卷
2012年2月,国务院同意发布新修订的《环境空气质量标准》增加了PM2.5监测指标.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000 001 米,那么数据0.000 002 5用科学记数法可以表示为( )
A. |
B. |
C. |
D. |
如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与折痕所成的角a的度数应为( )
| A.15°或30° | B.30°或45° | C.45°或60° | D.30°或60° |
北京市2001-2010年星级饭店客房出租率(%)的情况如下表:
| 年份 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
| 出租率 |
62 |
62 |
52 |
65 |
62 |
61 |
60 |
52 |
49 |
56 |
表中出租率(%)的中位数和众数分别为( )
A.61、62 B.62、62 C.61.5、62 D.60.5、62
如图,有6张形状、大小、质地均相同的卡片,正面分别印有北京精神——“爱国、创新、包容、厚德”的字样.背面完全相同,现将这6张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片恰好是“创新”的概率是( ) 
A. |
B. |
C. |
D. |
将二次函数 的图象如何平移可得到
的图象如何平移可得到 的图象( )
的图象( )
| A.向右平移2个单位,向上平移一个单位 |
| B.向右平移2个单位,向下平移一个单位 |
| C.向左平移2个单位,向下平移一个单位 |
| D.向左平移2个单位,向上平移一个单位 |
已知正方形纸片的边长为18,若将它按下图所示方法折成一个正方体纸盒,则纸盒的边(棱)长是( )
A. |
B. |
C. |
D. |


已知:如图是斜边为10的一个等腰直角三角形与两个半径为5的扇形的重叠情形,其中等腰直角三角形顶角平分线与两扇形相切,则图中阴影部分面积的和是 .
如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为 ,则电子跳蚤连续跳(
,则电子跳蚤连续跳( )步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳
)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳 步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳
步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳 步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为 ;第2012次电子跳蚤能跳到的圆圈内所标的数字为 .
步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为 ;第2012次电子跳蚤能跳到的圆圈内所标的数字为 .
已知一次函数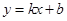 的图象与直线
的图象与直线 平行且经过点
平行且经过点 ,与
,与 轴、
轴、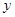 轴分别交于
轴分别交于 、
、 两点.
两点.
求此一次函数的解析式
点
 是坐标轴上一点,若△
是坐标轴上一点,若△ 是底角为
是底角为 的等腰三角形,求点
的等腰三角形,求点 的坐标.
的坐标.
列方程(组)解应用题:
如图是一块长、宽分别为60 m、50 m的矩形草坪,草坪中有宽度均为x m的一横两纵的甬道.
用含x的代数式表示草坪的总面积S ;
当甬道总面积为矩形总面积的
 %时,求甬道的宽
%时,求甬道的宽
如图,梯形纸片ABCD中,AD//BC,∠B=30º.折叠纸片使BC经过点A,点B落在点B’处,EF是折痕,且BE=EF=4, ∥
∥ .
.
求∠BAF的度数
当梯形的上底
 多长时,线段
多长时,线段 恰为该梯形的高?
恰为该梯形的高?
以下是根据全国 2011年国民经济和社会发展统计公报中的相关数据,绘制的统计图的一部分.请根据以上信息,解答下列问题:(产量相关数据精确到1万吨)请补全扇形统计图;
通过计算说明全国的粮食产量与上一年相比,增长最多的是 年
2011年早稻的产量为 万吨;
2008-2011这三年间,比上一年增长的粮食产量的平均数为多少万吨,若按此平均数增长,请你估计2012年的粮食产量为多少万吨.(结果保留到整数位)

已知:如图, 是⊙
是⊙ 的直径
的直径 上任意一点,过点
上任意一点,过点 作
作 的垂线
的垂线 ,
, 是
是 的延长线上一点,联结
的延长线上一点,联结 交⊙
交⊙ 于点
于点 ,且
,且 .
.
判断直线
 与⊙
与⊙ 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;若
 ,
, ,过点A作
,过点A作 的平行线
的平行线 交⊙
交⊙ 于点
于点 .求弦
.求弦 的长.
的长.
小阳遇到这样一个问题:如图(1),O为等边△ 内部一点,且
内部一点,且 ,求
,求 的度数.
的度数.


|
小阳是这样思考的:图(1)中有一个等边三角形,若将图形中一部分绕着等边三角形的某个顶点旋转60°,会得到新的等边三角形,且能达到转移线段的目的.他的作法是:如图(2),把△
 绕点A逆时针旋转60°,使点C与点B重合,得到△
绕点A逆时针旋转60°,使点C与点B重合,得到△ ,连结
,连结 . 则△
. 则△ 是等边三角形,故
是等边三角形,故 ,至此,通过旋转将线段OA、OB、OC转移到同一个三角形
,至此,通过旋转将线段OA、OB、OC转移到同一个三角形 中.
中. .
.已知:如图(3),四边形ABCD中,AB=AD,∠DAB=60°,∠DCB=30°,AC=5,CD=4.求四边形ABCD的面积.
已知:直线 分别与 x轴、y轴交于点A、点B,点P(
分别与 x轴、y轴交于点A、点B,点P( ,b)在直线AB 上,点P关于
,b)在直线AB 上,点P关于 轴的对称点P′ 在反比例函数
轴的对称点P′ 在反比例函数 图象上.
图象上.当a=1时,求反比例函数
 的解析式
的解析式设直线AB与线段P'O的交点为C.当P'C =2CO时,求b的值;
过点A作AD//y轴交反比例函数图象于点D,若AD=
 ,求△P’DO的面积.
,求△P’DO的面积. 
在△ 中,
中, ,
, 是底边
是底边 上一点,
上一点, 是线段
是线段 上一点,且
上一点,且
∠ .
.如图1,若∠
 ,猜想
,猜想 与
与 的数量关系为 ;
的数量关系为 ;如图2,若∠
 ,猜想
,猜想 与
与 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;若∠
 ,请直接写出
,请直接写出 与
与 的数量关系.
的数量关系.
 的算术平方根是( )
的算术平方根是( )



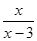 有意义的条件为 .
有意义的条件为 . ______ ________.
______ ________. .
. .
. 外部,DE交AC于F,若AD=AB,∠1=∠2=∠3.求证:BC=DE.
外部,DE交AC于F,若AD=AB,∠1=∠2=∠3.求证:BC=DE.
 ,求代数式
,求代数式 的值.
的值. x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左). ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由 个单位长度、每秒2
个单位长度、每秒2
 粤公网安备 44130202000953号
粤公网安备 44130202000953号