[江苏]2012届江苏省泰兴市黄桥区九年级中考一模数学试卷
将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
A. |
B. |
C. |
D. |
如图,现有一个圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )
| A.4cm | B.3cm | C.2cm | D.1cm |

已知反比例函数 的图象如图,则一元二次方程
的图象如图,则一元二次方程 根的情况是( )
根的情况是( )
| A.有两个不等实根 | B.有两个相等实根 | C.没有实根 | D.无法确定。 |
把长为8cm的矩形按虚线对折,按图中的虚线剪出一个直角梯形,找开得到一个等腰梯形,剪掉部分的面积为6cm2,则打开后梯形的周长是( )
A. cm cm |
B. cm cm |
C.22cm | D.18cm |
如图,正方形ABCD的边长是3cm,一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,它的方向是( )

A. B. C. D.
国家游泳中心“水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约为260000平方米,将260000用科学记数法表示应为
已知△ABC的面积为36,将△ABC沿BC的方向平移到△A/B /C /的位置,使B / 和C重合,连结AC / 交A/C于D,则△C /DC的面积为
如图,(甲)是四边形纸片ABCD,其中ÐB=120°,ÐD=50°。若将其右下角向内折出rPCR,恰使CP∥AB,RC∥AD,如图(乙)所示,则ÐC= °.
如图, 过
过 上到点
上到点 的距离为1,3,5,7,…的点作
的距离为1,3,5,7,…的点作 的垂线,分别与
的垂线,分别与 相交,得到图所示的阴影梯形,它们的面积依次记为
相交,得到图所示的阴影梯形,它们的面积依次记为 ….则
….则 ;通过计算可得
;通过计算可得

已知正比例函数 反比例函数
反比例函数 由
由 构造一个新函数
构造一个新函数 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
①该函数的图象是中心对称图形;
②当 时,该函数在
时,该函数在 时取得最大值-2;
时取得最大值-2;
③ 的值不可能为1;
的值不可能为1;
④在每个象限内,函数值 随自变量
随自变量 的增大而增大.
的增大而增大.
其中正确的命题是 .(请写出所有正确的命题的序号)
国民体质监测中心等机构开展了青少年形体测评.专家组随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:请将两幅统计图补充完整;
在这次形体测评中,一共抽查了 名学生,如果全市有10万名初中生,那么全市初中生中,三姿良好的学生约有 人;
根据统计结果,请你简单谈谈自己的看法.

有两个可以自由转动的均匀转盘 ,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘 ;
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).
用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60º.
求⊙O的直径;
若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
若动点E以2cm/s的速度从A点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动,设运动时间为
 ,连结EF,当
,连结EF,当 为何值时,△BEF为直角三角形.
为何值时,△BEF为直角三角形.

据悉,某市发改委拟于今年4月27日举行居民用水价格调整听证会,届时将有两个方案提供听证。如图(1),射线OA、射线OB分别表示现行的、方案一的每户每月的用水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;方案二如图(2)表格所示,每月的每立方米用水价格由该月的用水量决定,且第一、二、三级的用水价格之比为1︰1.5︰2(精确到0.01元后).写出现行的用水价是每立方米多少元?
求图(1)中m的值和射线OB所对应的函数解析式,并写出定义域;
若小明家某月的用水量是a立方米,请分别写出三种情况下(现行的、方案一和方案二)该月的水费b(用a的代数式表示);
小明家最近10个月来的每月用水量的频数分布直方图
如图(3)所示,估计小明会赞同采用哪个方案?请说明理由。 


如图,抛物线 与
与 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴相交于点
轴相交于点 ,顶点为
,顶点为 .
.
直接写出
 、
、 、
、 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;连接
 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点 ,点
,点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 交抛物线于点
交抛物线于点 ,设点
,设点 的横坐标为
的横坐标为 ;
;
①用含 的代数式表示线段
的代数式表示线段 的长,并求出当
的长,并求出当 为何值时,四边形
为何值时,四边形 为平行四边形?
为平行四边形?
②设 的面积为
的面积为 ,求
,求 与
与 的函数关系式.
的函数关系式.
定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径. 如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段 .
在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由. 友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由. 若此时AB=3,BD=
 ,求BC的长.
,求BC的长.


如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC = 4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.当x为何值时,△APD是等腰三角形?
若设BE=y,求y关于x的函数关系式
若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.



等腰直角△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.现△ABC以每秒2个单位的速度向右移动,同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大.当△ABC的边(BC边除外)与圆第一次相切时,点B移动了多少距离?
若在△ABC移动的同时,⊙O也以每秒1个单位的速度向右移动,则△ABC从开始移动,到它的边与圆最后一次相切,一共经过了多少时间?
在⑵的条件下,是否存在某一时刻,△ABC与⊙O的公共部分等于⊙O的面积?若存在,求出恰好符合条件时两个图形移动了多少时间?若不存在,请说明理由.

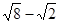 的结果是( )
的结果是( )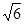
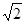
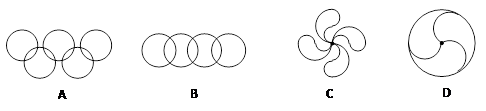


 中,自变量
中,自变量 的取值范围是
的取值范围是 的解集是
的解集是 为
为 的直径,弦
的直径,弦 于点
于点 连结
连结 若
若

 则
则

 -(-4)
-(-4) +
+ -2cos30°
-2cos30°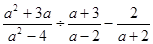 ,其中,
,其中,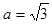 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号