如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC = 4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.当x为何值时,△APD是等腰三角形?
若设BE=y,求y关于x的函数关系式
若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.

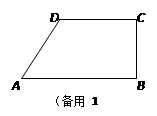

相关知识点
推荐套卷
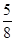 .求n的值
.求n的值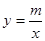 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.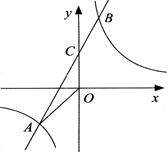
 的图象经过点A(2, -3),B(-1,12).
的图象经过点A(2, -3),B(-1,12).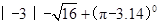 ;
;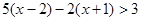
 粤公网安备 44130202000953号
粤公网安备 44130202000953号