[北京]2012届北京高考模拟系列试卷文科数学试卷一
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A. |
B. |
C. |
D. |

命题“存在 ,使
,使 <0,为假命题”是命题“
<0,为假命题”是命题“ ”的( )
”的( )
| A.充要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
如图,设A、B两点在河的两岸,一测量者在A的同侧所在的河岸边选定一点C,测出AC的距离为50m, 后,就可以计算出A、B两点的距离为( )
后,就可以计算出A、B两点的距离为( )
A. B.
B.
C. D.
D.

某校高中年级开设了丰富多彩的校本课程,甲、乙两班各随机抽取了5名学生的学分,用茎叶图表示(如右图). ,
, 分别表示甲、乙两班抽取的5名学生学分的标准差,则
分别表示甲、乙两班抽取的5名学生学分的标准差,则
 .(填“
.(填“ ”、“
”、“ ”或“=”).
”或“=”).
A. |
B. |
| C.= | D.不能确定 |

设双曲线 的两条渐近线与直线
的两条渐近线与直线 围成的三角形区域(包括边界)为D,P
围成的三角形区域(包括边界)为D,P 为D内的一个动点,则目标函数
为D内的一个动点,则目标函数 的最小值为( )
的最小值为( )
A. |
B. |
C.0 | D. |
观察下列等式:
1=1 13=1
1+2=3 13+23=9
1+2+3=6 13+23+33=36
1+2+3+4=10 13+23+33+43=100
1+2+3+4+5=15 13+23+33+43+53=225
……
可以推测:13+23+33+…+n3= 。( 用含有n的代数式表示)
用含有n的代数式表示)
已知向量 (
( >0),函数
>0),函数 的最小正周期为
的最小正周期为 。
。
(I)求函数 的单调增区间;(II)如果△ABC的三边a、b、c所对的角分别为A、B、C,且满足
的单调增区间;(II)如果△ABC的三边a、b、c所对的角分别为A、B、C,且满足 求
求 的值。
的值。
已知关于 的一元二次函数
的一元二次函数
(Ⅰ)设集合 和
和 ,分别从集合
,分别从集合 和
和 中随机取一个数作为
中随机取一个数作为 和
和 ,求函数
,求函数 在区间[
在区间[ 上是增函数的概率;
上是增函数的概率;
(Ⅱ)设点 是区域
是区域 内的随机点,记
内的随机点,记 有两个零点,其中一个大于
有两个零点,其中一个大于 ,另一个小于
,另一个小于
 ,求事件
,求事件 发生的概率
发生的概率
如图,已知直四棱柱 的底面是直角梯形,
的底面是直角梯形, ,
, ,
, ,
, 分别是棱
分别是棱 ,
, 上的动点,且
上的动点,且 ,
, ,
, .
.
(Ⅰ)证明:无论点 怎样运动,四边形
怎样运动,四边形 都为矩形;
都为矩形;
(Ⅱ)当 时,求几何体
时,求几何体 的体积。
的体积。
 ,则
,则 =( )
=( )



 ,则
,则 等于 ( )
等于 ( )

 中,首项
中,首项 公差
公差 ,若
,若 ,则
,则 ( )
( )



 和
和 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( )



 与
与 轴,
轴, 轴分别交于
轴分别交于 两点,若动点
两点,若动点 在线段
在线段 上,则
上,则 的最大值为 ( )
的最大值为 ( )

 的图象大致是( )
的图象大致是( )
 ,则对任意
,则对任意 ,若
,若 ,下列不等式成立的是( )
,下列不等式成立的是( )



 ,其中
,其中 为实数,
为实数, ,
, ,
, ,若
,若 ,则
,则 ;
;
 在直线
在直线 上,过点
上,过点 与曲线
与曲线 只有一个公共点
只有一个公共点 ,则
,则 的最小值为__________;
的最小值为__________; 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且 ,
, 。
。 求数列
求数列 的前n项和Sn。
的前n项和Sn。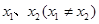 是函数
是函数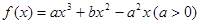 的两个极值点。
的两个极值点。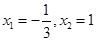 ,求函数
,求函数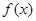 的解析式;
的解析式; ,求
,求 的最大值。
的最大值。
 的离心率为
的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 。
。 的方程;
的方程; 与椭圆
与椭圆 、
、 两点。
两点。 中点的横坐标为
中点的横坐标为 ,求斜率
,求斜率 的值;
的值; ,求证:
,求证: 为定值
为定值 粤公网安备 44130202000953号
粤公网安备 44130202000953号