[河北]2012届河北省石家庄市高中毕业班教学质量检测理科数学
已知全集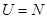 ,集合
,集合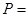 {1,2,3,4,5},
{1,2,3,4,5}, {1,2,3,6,8},则
{1,2,3,6,8},则 =
=
| A.{1,2,3} | B.{4,5} | C.{6,8} | D.{1,2,3,4,5} |
图示是计算1+ +
+ +…+
+…+ 值的程序框图,则图中(1)、(2)处应填写的语句分别是
值的程序框图,则图中(1)、(2)处应填写的语句分别是
A. ? ? |
B. ? ? |
C. ? ? |
D. ? ? |

已知函数 ,下面结论错误的是
,下面结论错误的是
A.函数 的最小正常周期为 的最小正常周期为 |
B.函数 可由 可由 向左平移 向左平移 个单位得到 个单位得到 |
C.函数 的图象关于直线 的图象关于直线 对称 对称 |
D.函数 在区间[0, 在区间[0, ]上是增函数 ]上是增函数 |
已知定义域为R的函数 是奇函数,当
是奇函数,当 时,
时, |
| |-
|- ,且对
,且对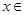 R,恒有
R,恒有 ,则实数
,则实数 的取值范围为
的取值范围为
| A.[0,2] | B.[- , , ] ] |
C.[-1,1] | D.[-2,0] |

学校要安排4名学生在周六、周日参加社会实践活动,每天至少1人,则学生甲被
安排在周六的不同排法的种数为 (用数学作答).
(本小题满分12分)
已知数列{ }为公差不为零的等差数列,
}为公差不为零的等差数列, =1,各项均为正数的等比数列{
=1,各项均为正数的等比数列{ }的第1
}的第1
项、第3项、第5项分别是 、
、 、
、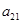 .
.
(I )求数列{
)求数列{ }与{
}与{ }的通项公式;
}的通项公式;
(Ⅱ)求数列{
 }的前
}的前 项和.
项和.
(本小题满分l2分)
如图,在多面体ABCDEF中,ABCD为菱形, ABC=60
ABC=60 ,E
,E C
C 面ABCD,FA
面ABCD,FA 面ABCD,G
面ABCD,G
为BF的中点,若EG//面ABCD
(I)求证:EG 面ABF
面ABF
(Ⅱ)若AF=AB,求二面角B—EF—D的余弦值
(本小题满分1 2分)
2分)
某班甲、乙两名同学参加l00米达标训练,在相同条件下两人l0次训练的成绩(单位:秒)
如下:
(I)请画出适当的统计图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩
的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答
结论). (Ⅱ)从甲、乙两人的10次成绩中各随机抽取一次,求抽取的成绩中至少有一个低
于12.8秒的概率.
(III)经过对甲、乙两位同学的若干次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]
之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率
(本小题满分12分)
点P为圆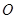 :
: (
(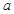 >0)
>0) 上一动点,PD
上一动点,PD
 轴于D点,记线段PD的中点M的运
轴于D点,记线段PD的中点M的运
动轨迹为曲线C.(I)求曲线C的方程; (II)若动直线 与曲线C交于A、B两点,当△OAB(O是坐标原点)面积取得最大值,且最大值为1时,求
与曲线C交于A、B两点,当△OAB(O是坐标原点)面积取得最大值,且最大值为1时,求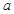 的值.
的值.
(本小题满分l2分) 已知函数
已知函数 ,
, ∈R.
∈R.
(I)讨论函数 的单调性;
的单调性;
(Ⅱ)当 时,
时, ≤
≤ 恒成立,求
恒成立,求 的取值范围
的取值范围
(本小题满分10分)选修4—1:几何证明选讲
如图,AB为圆 的直径,P为圆
的直径,P为圆 外一点,过P点作PC
外一点,过P点作PC AB于C,交圆
AB于C,交圆 于D点,PA
于D点,PA
交圆 于E点,BE交PC于F点.(I)求证:
于E点,BE交PC于F点.(I)求证: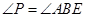 ;(Ⅱ)求证:
;(Ⅱ)求证:

(本小题满分10分)选修4—4:坐标系与参数方程
在平面直角坐标系 中,以原点
中,以原点 为极点,
为极点, 轴为极轴建立极坐标系,曲线C1的方程
轴为极轴建立极坐标系,曲线C1的方程
为 (
( 为参数),曲线C2的极坐标方程为:
为参数),曲线C2的极坐标方程为: ,若曲线C1与
,若曲线C1与
C2相交于A、B两点. (I)求|AB|的值;(Ⅱ)求点M(-1,2)到A、B两点的距离之积.
 ,则
,则 =
=
 +
+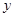 轴上的双曲线的离心率为
轴上的双曲线的离心率为 ,则它的渐近线方程为
,则它的渐近线方程为



 ,使得
,使得 ;
; ,使得
,使得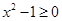 .以下命题为真命题的为
.以下命题为真命题的为



 (5,4),动点
(5,4),动点 (
( ,
,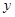 )满足
)满足 ,则|
,则| |的最小值为
|的最小值为

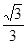



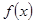 满足
满足 ,其导函数
,其导函数 的图象如下图,则
的图象如下图,则 轴所围成的封闭图形的面积为
轴所围成的封闭图形的面积为





 +
+

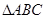 中,
中, 是
是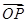 =
=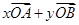 ,其中
,其中 ,
, ,动点
,动点
 的轨迹所覆盖的面积为
的轨迹所覆盖的面积为




 的定义域为 .
的定义域为 . 、
、 、
、 为两两垂直的单位向量,非零向量
为两两垂直的单位向量,非零向量 ,若向量
,若向量 与向量
与向量 、
、 、
、 ,则
,则 .
. 作抛物线
作抛物线 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,若
,若 中点的纵坐标为6,则抛物线的方程为 .
中点的纵坐标为6,则抛物线的方程为 .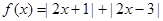 .(I)求不等式
.(I)求不等式 ≤6的解集;(Ⅱ)若关于
≤6的解集;(Ⅱ)若关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号