[吉林]2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
已知不等式组 表示的平面区域为M,若直线
表示的平面区域为M,若直线 与平面区域M有公共点,则
与平面区域M有公共点,则 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
设数列 是单调递增的等差数列,前三项的和为12,前三项的积为48,则它的首项是
是单调递增的等差数列,前三项的和为12,前三项的积为48,则它的首项是
| A.1 | B.2 | C. |
D.4 |
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
 ,
, 为椭圆
为椭圆 的两个焦点,过
的两个焦点,过 作椭圆的弦
作椭圆的弦 ,若
,若 的周长为16,椭圆的离心率
的周长为16,椭圆的离心率 ,则椭圆的方程是
,则椭圆的方程是
A. |
B. |
C. |
D. |
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
已知点P是抛物线 = 2x上的动点,过点P作y轴垂线PM,垂足为M, 点A的坐标是
= 2x上的动点,过点P作y轴垂线PM,垂足为M, 点A的坐标是 ,则| PA | + | PM |的最小值是
,则| PA | + | PM |的最小值是
A. |
B.4 | C. |
D.5 |
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
锐角△ABC中,a、b、c分别是三内角A、B、C的对边,如果B=2A,则 的取值范围是
的取值范围是
| A.(-2,2) | B.(0,2) | C.( , , ) ) |
D.( ,2) ,2) |
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
已知 是椭圆
是椭圆 的两个焦点, 若存在点P为椭圆上一点, 使得
的两个焦点, 若存在点P为椭圆上一点, 使得 , 则椭圆离心率
, 则椭圆离心率 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
如图,设A,B两点在河的两岸,一测量者在A的同侧,在A所在的河岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°后,则A,B两点的距离
为 m
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
设数列 的前n项和为
的前n项和为 ,令
,令 ,称
,称 为数列
为数列 ,
, ,……,
,……, 的“和平均数”,已知数列
的“和平均数”,已知数列 ,
, ,……,
,……, 的“和平均数”为2012,那么数列2,
的“和平均数”为2012,那么数列2, ,
, ,……,
,……, 的“和平均数”为
的“和平均数”为
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
设命题 :实数
:实数 满足
满足 ,其中
,其中 ,命题
,命题 :实数
:实数 满足
满足 .
.
(1)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围
的取值范围
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
如图,已知椭圆
 (a>b>0)的离心率
(a>b>0)的离心率 ,过顶点A、B的直线与原点的距离为
,过顶点A、B的直线与原点的距离为 .
.
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
如图,三棱柱 中,
中, 面
面 ,
, =
= ,
, ,
,  为
为 的中点,
的中点, 为
为 的中点:
的中点:
(1)求直线 与
与 所成的角的余弦值;
所成的角的余弦值;
(2)在线段 上是否存在点
上是否存在点 ,使
,使
 平面
平面 ,若存在,求出
,若存在,求出 ;若不存在,说明理由。
;若不存在,说明理由。
来源:2011-2012学年度吉林省吉林市高二上学期期末理科数学试卷
 的准线方程为
的准线方程为



 满足
满足 ,则此数列的通项
,则此数列的通项 等于
等于



 ,则下列不等式中正确的是
,则下列不等式中正确的是



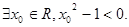 ”的否定为
”的否定为
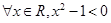
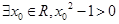
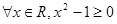
 的实轴长、虚轴长、焦距成等差数列,则双曲线的离心率是
的实轴长、虚轴长、焦距成等差数列,则双曲线的离心率是



 ,且
,且 ,若
,若 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是



 , 并且焦距为20,则双曲线的标准方程为
, 并且焦距为20,则双曲线的标准方程为  为棱长为1的正方体
为棱长为1的正方体 内(含正方体表面)任意一点,则
内(含正方体表面)任意一点,则 的最大值为
的最大值为  中,公比
中,公比 ,数列的前n项和为
,数列的前n项和为 ,若
,若 ,求数列
,求数列 ,
, ,B=45°, 求A、C及c .
,B=45°, 求A、C及c . :
: ,焦点为
,焦点为 ,其准线与
,其准线与 轴交于点
轴交于点 ;椭圆
;椭圆 :分别以
:分别以 为左、右焦点,其离心率
为左、右焦点,其离心率 ;且抛物线
;且抛物线 的一个交点记为
的一个交点记为 .
. 时,求椭圆
时,求椭圆
 经过椭圆
经过椭圆 与抛物线
与抛物线 两点,若弦长
两点,若弦长 等于
等于 的周长,求直线
的周长,求直线 粤公网安备 44130202000953号
粤公网安备 44130202000953号