[四川]2011-2012学年四川省巴中市四县中高二上学期期末考试理科数学
若点A 关于
关于 轴的对称点是B
轴的对称点是B ,则
,则 的值依次是( )
的值依次是( )
| A.1,-4,9 | B.2,-5,-8 | C.-3,-5,8 | D.2,5,8 |
已知椭圆 内有一点P
内有一点P ,以P为中点作弦MN,则直线MN的方程是( )
,以P为中点作弦MN,则直线MN的方程是( )
A. |
B. |
C. |
D. |
给出以下四个命题
①如果直线 和平面
和平面 内无数条直线垂直,则
内无数条直线垂直,则 ⊥
⊥ ;
;
②如果平面 //
// ,直线
,直线 ,直线
,直线 ,则
,则 、
、 两条直线一定是异面直线;
两条直线一定是异面直线;
③如果平面 上有不在同一直线上的三个点,它们到平面
上有不在同一直线上的三个点,它们到平面 的距离都相等,那么
的距离都相等,那么 //
// ;
;
④如果 、
、 是异面直线,则一定存在平面
是异面直线,则一定存在平面 过
过 且与
且与 垂直
垂直
其中真命题的个数是:( )
| A.3个 | B.2个 |
| C.1个 | D.0个 |
如图1,正四棱锥相邻两侧面形成的二面角为θ,则θ的取值范围是
A.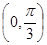 |
B. |
C. |
D.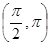 |
已知抛物线 ,直线
,直线 过定点
过定点 ,直线
,直线 与抛物线只有一个公共点时,直线
与抛物线只有一个公共点时,直线 的斜率是__________。
的斜率是__________。
已知圆系 。圆C过
。圆C过 轴上的点A,线段MN是圆C在
轴上的点A,线段MN是圆C在 轴上截得的弦。设
轴上截得的弦。设 ,对于下列命题:
,对于下列命题:
①不论t取何实数,圆心C始终在曲线 上;
上;
②不论t取何实数,弦MN的长为定值1;
③不论t取何实数,圆系C的所有圆都与直线 相切;
相切;
④式子 的取值范围是
的取值范围是 。
。
其中所有正确命题的序号是________________。
(本题12分)已知△ABC的三个顶点坐标分别为A , B
, B ,C
,C ,
,
(Ⅰ)求AC边上的中线所在直线方程;
(Ⅱ)求AB边上的高所在直线方程;
(Ⅲ)求BC边的垂直平分线的方程。
(本题12分)求过两圆 的交点,
的交点,
(Ⅰ)且过M 的圆
的圆 的方程;
的方程;
(Ⅱ)且圆心在直线 上的圆
上的圆 的方程。
的方程。
((本题12分)如图2,在棱长为1的正方体ABCD—A1B1C1D1中,点E、F、G分别是DD1、BD、BB1的中点。
(Ⅰ)求直线EF与直线CG所成角的余弦值;
(Ⅱ)求直线C1C与平面GFC所成角的正弦值;
(Ⅲ)求二面角E—FC—B的余弦值。
((本题12分)已知P与平面上两定点A ,B
,B 连线的斜率的积为定值
连线的斜率的积为定值 ,
,
(Ⅰ)试求动点P的轨迹方程C;
(Ⅱ)设直线 与曲线C交于M、N两点,当|MN|=
与曲线C交于M、N两点,当|MN|= 时,求直线
时,求直线 的方程。
的方程。
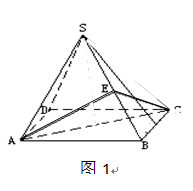
((本题14分)如图3,四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD= 。
。
(Ⅰ)求证:MN//平面PAD;
(Ⅱ)求证:平面PMC⊥平面PCD;
(Ⅲ)若二面角P—MC—A是60°的二面角,求四棱锥P—ABCD的体积。


 ,则抛物线的标准方程是( )
,则抛物线的标准方程是( )



 平行,则它们之间的距离是( )
平行,则它们之间的距离是( )


 ,直线
,直线 ,若
,若 //
// ,则
,则 等于( )
等于( ) 被圆
被圆 截得的弦长是( )
截得的弦长是( )

 与圆
与圆 的位置关系是( )
的位置关系是( ) 的渐近线方程是_________________。
的渐近线方程是_________________。 的圆
的圆 的切线方程是_____________。
的切线方程是_____________。 的离心率是
的离心率是 ,则双曲线
,则双曲线 =1的离心率是______。
=1的离心率是______。 C
C 是△ABC的两个顶点,且
是△ABC的两个顶点,且 ,则顶点A的轨迹方程是___________。
,则顶点A的轨迹方程是___________。 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4
,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。 ;
; ,使得
,使得 恒成立?若存在,求
恒成立?若存在,求
 粤公网安备 44130202000953号
粤公网安备 44130202000953号