[四川]2012届四川省绵阳市高三第二次月考理科数学试卷

已知复数（其中i为虚数单位)，则复数的虚部是

A．

B．

C．

D．

“函数f(X)在点处连续”是“函数f(X)在点处有极限”的

平面内动点P(x,y)与A(-2,0)，B(2, 0)两点连线的斜率之积为，则动点P的轨迹方程为 

A．	B．
C．	D．

在平行四边形ABCD中，，已知，则=

A．

B．

C．

D．

函数的图象大致是

直线l与抛物线交于A,B两点;线段AB中点为，则直线l的方程为

A．	B．、
C．	D．

已知数列满足，则=

A．

B．

C．

D．

把函数的图象按向暈平移后得到函数的图象,则函数在区间上的最大值为

A．O,

B．1

C．

D．-1

已知曲线和曲线（为参数）关于直线l₁.对称,直线l₂过点旦与l₁的夹角为60° ,则直线l₂的方程为

A．	B．
C．	D．

已知F₁,F₂分别是双曲线（a>0，b>0)的左、右焦点，过F₂且平行于y轴的直线交双曲线的渐近线M，N两点.若ΔMNF₁为锐角三角形,则该双曲线的离心率的取值范围是

A．

B．

C．

D．

己知关于x的方程的两根分别为椭圆和双曲线的离心率.记分别以m、n为横纵坐标的点P(m，n)表示的平面区域为D,若函数的图象上存在区域D上的点,则实数a的取值范围为

A．

B．

C．

D．

若实数x,y满足方程组则=

A．0

B．

C．

D．1

计算= __________

已知扇形AOB（为圆心角）的面积为，半径为2,则的面积为_______

已知为抛物线，上的动点,点N的坐标为，则的最小值为_______

对于具有相同定义域D的函数f(x)和g(x),若对任意的，都有，则称f(x)和g(x)在D上是“密切函数”.给出定义域均为的四组函数如下
①；  ②；
③（其中e为自然对数的底数),；④.
其中,函数f(x)和g(x)在D上为“密切函数”的是_______

已知向量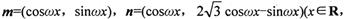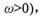函数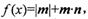且最小正周期为.
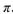(I)求函数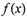的最大值,并写出相应的X的取值集合；
(II)在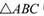中，角A，B, C所对的边分别为a, b,c,且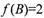,c=3,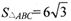，求b的值.

为备战2012年伦敦奥运会，爾家篮球队分轮次迸行分项冬训.训练分为甲、乙两组,根据经验，在冬训期间甲、乙两组完成各项训练任务的概率分别为和P(P>0)假设每轮训练中两组都各有两项训练任务需完成，并且每项任务的完成与否互不影响.若在一轮冬训中，两组完成训练任务的项数相等且都不小于一项，则称甲、乙两组为“友好组”
(I)若求甲、乙两组在完成一轮冬训中成为“友好组”的概率_;
(II)设在6轮冬训中，甲、乙两组成为“友好组”的次数为，当时,求P的取值范围.

已知圆C的半径为1,圆心C在直线l_1:上，且其横坐标为整数，又圆C截直线所得的弦长为•
(I )求圆C的标准方程;
(II)设动点P在直线上，过点P作圆的两条切线PA, PB,切点分别为A ,B求四边形PACB面积的最小值.

已知数列{a_n}的前n项和，数列为等比数列，且首项b₁和公比q满足：
(I)求数列的通项公式;
(II)设，记数列的前n项和，若不等式对任意恒成立,求实数的最大值.

已知椭圆的左、右焦点分别为,离心率,A为右顶点,K为右准线与X轴的交点，且.
(I)求椭圆的标准方程；
(II)设椭圆的上顶点为B，问是否存在直线l,使直线l交椭圆于C，D两点，且椭圆的左焦点巧恰为ΔBCD的垂心?若存在,求出l的方程_r若不存在,请说明理由.

已知函数
(I)若直线l₁交函数f(x)的图象于P,Q两点，与l₁平行的直线与函数的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
(II)若不等式恒成立,求实数a的取值范围；
(III)求证:〔其中, e为自然对数的底数）