为备战2012年伦敦奥运会,爾家篮球队分轮次迸行分项冬训.训练分为甲、乙两组,根据经验,在冬训期间甲、乙两组完成各项训练任务的概率分别为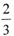 和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
(I)若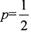 求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
(II)设在6轮冬训中,甲、乙两组成为“友好组”的次数为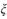 ,当
,当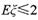 时,求P的取值范围.
时,求P的取值范围.
推荐套卷
为备战2012年伦敦奥运会,爾家篮球队分轮次迸行分项冬训.训练分为甲、乙两组,根据经验,在冬训期间甲、乙两组完成各项训练任务的概率分别为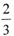 和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
(I)若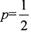 求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
(II)设在6轮冬训中,甲、乙两组成为“友好组”的次数为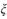 ,当
,当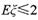 时,求P的取值范围.
时,求P的取值范围.