[安徽]2012届安徽省淮北市高三第一次模拟考试文科数学

设全集U=R，集合A={x|O<x<l}，B={x|O<x<3），那么（）∩B等于    (    )

若，则复数z对应的点在    (    )

若丑∈R，则“a>l”是“|a|>l”的    (    )

若等差数列{a_n}的公差d<0，且a₁+a_ll =0，则数列{a_n}的前n项和S_n取得最大值时的项数n是    (    )

若某多面体的三视图（单位：cm）如右图所示，则此多面体外接球的表面积是(    )

A．cm2

B．2cm2

C．3cm2

D．4cm2

若圆C的半径为1，圆心在第一象限，且与直线4x-3y=0和x轴都相切，则该圆的标准方程是    (    )

在边长为1的等边△ABC中，设，，则等于

A．

B．

C．

D．

已知m、n表示直线，α、β、γ表示平面，给出下列四个命题，其中真命题为    (    )
①α∩β=m，n≌αn⊥m则a⊥β ②a⊥β，a∩γ=m，β∩γ="n" 则n⊥m
③m⊥a，m⊥β，则α∥β   ④m⊥α，n⊥β，m⊥n，则α⊥β

已知O<m<l<n，关于x的不等式O<m^x-n^x<1的解集是{x|-l<x<O}，则m，n满足的关系是    (  )

A．	B．
C．	D．m，n的关系不能确定

定义方程的实数根x₀叫做函数f(x)的“新驻点”，如果函数g(x)=x，h(x)=lnx,Ф(x)=cosx(x∈(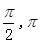)）的“新驻点”分别为α,β,γ那么α,β,γ的大小关系是    (    )

已知命题p：存在n∈N，使2ⁿ>1 000，则﹁p为________．

设O为坐标原点，点M坐标为(2，1)，点N(x，y)满足不等式组：
则的最大值为____________．

若执行如图所示的程序框图，则输出的i的值为________．

已知a+b=1，对任意的实数a,b∈(o，+∞)，那么的最小
值为________．

对于函数，有以下四个命题：
①f(x)为奇函数；②f(x)的最小正周期为；③f(x)在()上单调递减；④是f(x)的一条对称轴，其中真命题有     （把所有正确命题的序号都填上）

在△ABC中，角A，B，C所对的边分别为a，b，c，角A，B，C依次成等差数列．
(1)若b²=ac，试判断△ABC的形状；
(2)若△ABC为钝角三角形，且a>c，求的取值范围．

某工厂有甲、乙两个生产小组，每个小组各有四名工人，某天该厂每位工人的生产情况如下表．

(1)用茎叶图表示两组的生产情况；
(2)求乙组员工生产件数的平均数和方差；
(3)分别从甲、乙两组中随机选取一名员工的生产件数，求这两名员工的生产总件数为19的概率．
（注：方差，其中为x₁，x₂，…，x_n的平均数）

已知a为常数，且a≠O，函数f(x)=ax+axlnx+2.
(1)求函数f(x)的单调区间；
(2)当a=1时，若直线y=t与曲线y=f(x)（z∈[]有公共点，求t的取值范围，

如图所示，三棱柱ABC—A₁B₁C₁中，AB=AC=AA₁=2，面ABC₁上面AA_lC_lC,∠AA_lC_l=∠BAC₁=60⁰，AC₁与A₁C相交于0，E为BC的中点．
(1)求证.OE∥面AA_l B_lB；
(2)求证：B0⊥面AA₁C₁C;
(3)求三棱锥C—AEC₁的体积．

.已知椭圆C的中点在原点，焦点在x轴上，离心率等于，它的一个顶点恰好是抛物线的焦点．
(1)求椭圆C的方程;
(2)P(2，3)，Q(2，-3)是椭圆上两点，A、B是椭圆上位于直线PQ两侧的两动点，若直线AB的斜率为，求四边形APBQ面积的最大值．

.(本题满分13分）设函数，方程f(x)=x有唯一的解，
已知f(x_n)=x_n+1(n∈N﹡)且f(x_l)=．
(1)求证：数列{）是等差数列；
(2)若，求Sn=b₁+b₂+b₃+…+b_n
(3)在(2)的条件下，是否存在最小正整数m，使得对任意n∈N﹡，有成立，若存在，求出m的值；若不存在，请说明理由。