[浙江]2010-2011年浙江省嵊州市九年级上学期期末考试数学卷
已知反比例函数 ,则下列点中在这个反比例函数图象上的点是 ( )
,则下列点中在这个反比例函数图象上的点是 ( )
A.( ,1) ,1) |
B.(1,-2) | C.( -1, -2) | D.(2,2) |
.在Rt△ABC中,∠C=900,BC=1,AC=2,则tanA的值是 ( )
A. |
B.2 | C. |
D. |
如图,已知D、E分别是 的AB、 AC边上的点,
的AB、 AC边上的点,
 那么
那么 等于(
等于( 
| A.1 :3 | B.1 :4 |
| C.1 :9 | D.1 :16 |
.如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.则图中相似三角形(相似比为1 除外)有( )

A 一对 B 二对 C 三对 D 四对
.已知(x1,y1),B(x2,y2),C(x3,y3)是反比例函数 的图象上的三个点,并且x1<x2<0,x3>0,则y1,y2,y3的大小关系是 ( )
的图象上的三个点,并且x1<x2<0,x3>0,则y1,y2,y3的大小关系是 ( )
| A.y1<y2<y3, | B.y2<y3<y1, | C.y3<y2<y1, | D.y3<y1<y2, |
已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=450。给出以下五个结论:①∠EBC=22.50,;②BD=DC;③AE=2EC;④劣弧 是劣弧
是劣弧 的2倍;⑤DE=DC。其中正确结论有( )
的2倍;⑤DE=DC。其中正确结论有( )
A 2个 B 3个 C 4个 D 5个
.已知二次函数 的图象如图所示,有下列4个结论:①
的图象如图所示,有下列4个结论:① >0;②
>0;② >0;③
>0;③ <0;④
<0;④ >0;其中正确的结论有( )
>0;其中正确的结论有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
.如图,在正方形ABCD中,M、N分别是边CD、DA的中点,则sin∠MBN的值是( )

A. B.
B. C.
C. D.
D.
.如图,点P是反比例函数图象上一点,PM ⊥x轴于M,若△POM的面积为5,则反比例函数的解析式为 。
.已知二次函数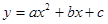 (
( ,
,  ,
, 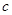 为常数),
为常数), 与
与 的部分对应值如下表,则当x满足的条件是 时,
的部分对应值如下表,则当x满足的条件是 时, >0.
>0.
| x |
-2 |
-1 |
0 |
1 |
2 |
3 |
| y |
-6 |
-6 |
0 |
2 |
0 |
-6 |
.如图,在等边△ABC中,P是BC边上一点,D为AC上一点,且∠APD=60°,BP=3,CD=2,则△CPD,△BAP,△APD的面积比为 。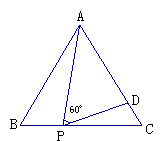
.(本小题满分8分)
已知二次函数的图像经过点(0,-3),且顶点坐标为(-1,-4)。(1)求该二次函数的解析式;
(2)设该二次函数的图像与x轴的交点为A、B,与
 轴的交点为C,求△ABC的面积。
轴的交点为C,求△ABC的面积。
(本小题满分10分)
已知:如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0)。直线BC交反比例函数的图象于点D。
(1)求该反比例函数的解析式和点B的坐标;
(2)求点D的坐标。
.(本小题满分10分)
如图,已知扇形的半径为15cm,∠AOB=120°。
(1)求扇形的面积;
(2)用这扇形围成圆锥的侧面,求该圆锥的高和底面半径。
.(本小题满分10分)
热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,A处与高楼的水平距离为60m,这栋高楼有多高?(结果精确到0.1m,参考数据: )
)

在矩形ABCD中,AB=4,BC=10,点M在BC上。
(1)若BM=3时,求点D到直线AM的距离;
(2)若AM⊥DM,求BM的长。
.(本小题满分12分)
如图,已知在⊙O中,直径AB=10,点E是OA上任意一点,过E作弦CD⊥AB,点F是弧BC上一点,连结AF交CE于H,连结AC、CF、BF。
(1)请你找出图中的相似三角形,并对其中的一对相似三角形进行证明;
(2)若AE:BE=1:4,求CD长。
(3)在(2)的条件下,求
 的值。
的值。
 的顶点坐标是( )
的顶点坐标是( )


 ,其图象在第二、四象限内,则k的值可为( )
,其图象在第二、四象限内,则k的值可为( ) ,且
,且 ,则
,则 。
。 的斜坡向下行驶50米,则它距离地面的垂直高度下降了 米.
的斜坡向下行驶50米,则它距离地面的垂直高度下降了 米.
 中,直径CD⊥弦AB,且
中,直径CD⊥弦AB,且 ,则
,则 的度数是 。
的度数是 。
 60°一
60°一 cos45°
cos45°
 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积; 粤公网安备 44130202000953号
粤公网安备 44130202000953号