[福建]2006-2007年福建省福州市九年级第一学期期末考试数学卷
如图,点A、B、C在⊙O上,∠AOC=70°,则∠ABC的度数为
A、10°; B、20°; C、35°; D、55°.
方程x(x-1)=0的解是
A、x=0; B、x=1; C、x=0或x=-1; D、x=0或x=1.
气象台预测“本市降雨的概率是80%”,对预测的正确理解是
A、本市明天有80%的地区降雨; B、本市明天将有80%的时间降雨;
C、明天出行不带雨具会淋雨; D、明天出行不带雨具肯定会淋雨.
已知x=1是一元二次方程x2-2mx+1=0的一个解,则m的值是
A、1; B、0; C、0或1; D、0或-1.
如图,在平面直角坐标系中,A点坐标为(-4,3),将线段OA绕原点O顺时针旋转90°得到OA',则点A'的坐标是
A、(-4,3); B、(-3,4); C、(3,-4); D、(4,-3).
抛物线y=x2-4x+1的顶点坐标是
A、(-2,13); B、(2,-3); C、(2,5); D、(-2,-3).
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则r与R之间的关系是
A、R=2r; B、 ; C、R=3r; D、R=4r.
; C、R=3r; D、R=4r.
如图,在Rt△ABC中,∠C=90°,CDEF为内接正方形,若AE=2cm,BE=1cm,则图中阴影部分的面积为
A、1cm2; B、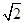 cm2; C、
cm2; C、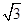 cm2; D、2cm2.
cm2; D、2cm2.
图是一个被分成6个扇形可自由转动的转盘,转动转盘,当转盘停止后,指针指向白色区域的概率是____________.
如图,矩形ABCD中,截去正方形ABMN后,矩形MCDN与原矩形ABCD相似.若正方形ABMN的边长为1,AD为x,则可列出的方程是__________________.
已知抛物线y=ax2+bx+c的部分图象如图所示,若y>0,则x的取值范围是_____________.
(本题满分12分)
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1) 填空:∠ABC=___________°,BC=_________;
(2) 判断△ABC与△DEF是否相似,并证明你的结论.
(本题满分12分)已知关于x的一元二次方程x2-3x+m=0.(1) 当m为何值时,方程有两个相等的实数根;
(2) 当
 时,求方程的正根.
时,求方程的正根.
(本题满分12分)
节假日,小明和哥哥在水族馆看完海洋动物后,参加了出口处的抽奖活动.游戏的规则如下:每张门票只可摸球一次,每次从装有大小形状相同的2个白球和1个红球的盒子中,随机摸出一个球,若摸出的是红球,则获得一份奖品.(1) 求每次摸球中奖的概率?
(2) 小明想:我有二张票,中奖的概率就翻一倍.你认为小明的思考正确吗?请用列表法或画树形图分析说明.
(本题满分12分)已知AB是⊙O的一条弦,CD是⊙O的直径,CD⊥AB,垂足为K.现取一块三角板,把它的一个锐角顶点固定在点C处,该锐角的两边(从左到右)与直线AB和圆分别相交于E、F和G、H.
(1) 若∠C的一边过圆心,请选择图10-1或图10-2所示,求证: △CEF∽△CHG;
(2) 若∠C的边不过圆心,在图10-3中补全一种示意图,请你观察所画的图形,并判断(1)中的结论是否仍然成立?若成立,给予证明;若不成立,请说明理由.
(本题满分14分)
如图是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.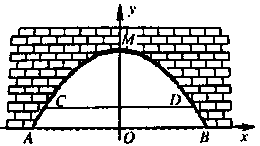
(1) 求出抛物线的解析式;
(2) 经过测算,水面离拱桥顶端1.5m时为警戒水位.某次洪水到来时,小明用仪器测得水面宽为10m,请你帮助小明算一算,此时水面是否超过警戒水位.
(本题满分14分)(1) 如图所示的网格坐标系中,顶点在格点上的矩形ABCD被分割成四块全等的小矩形①、②、③、④,并经过一次或二次变换拼成正方形A1B1C1D1.试写出小矩形从①→⑤、③→⑦一种变换过程;

(2) 对任意一个矩形按(1)的方式实施分割、变换后拼成正方形.试探究矩形ABCD的周长与面积分别与正方形A1B1C1D1的周长与面积的大小关系?并用代数方法验证你的结论.
 ; D、
; D、 .
. ; B、
; B、 ; C、3; D、
; C、3; D、 .
. =______________.
=______________.
 ,
, ,求
,求 的值.
的值.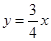 的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.
的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.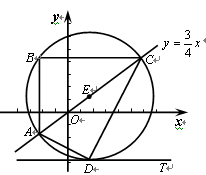
 粤公网安备 44130202000953号
粤公网安备 44130202000953号