(本题满分12分)
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.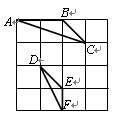
(1) 填空:∠ABC=___________°,BC=_________;
(2) 判断△ABC与△DEF是否相似,并证明你的结论.
相关知识点
推荐套卷
(本题满分12分)
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1) 填空:∠ABC=___________°,BC=_________;
(2) 判断△ABC与△DEF是否相似,并证明你的结论.