[浙江]2012届浙江省台州市四校高三第一次联考理科数学试卷
设 是非空集合,定义
是非空集合,定义 ={
={ 且
且 },己知
},己知
 ,则
,则 等于 ( )
等于 ( )
| A.(2,+∞) | B.[0,1]∪[2,+∞) |
| C.[0,1)∪(2,+∞) | D.[0,1]∪(2,+∞) |
已知命题 :抛物线
:抛物线 的准线方程为
的准线方程为 ;命题
;命题 :若函数
:若函数 为偶函数,则
为偶函数,则 关于
关于 对称.则下列命题是真命题的是 ( )
对称.则下列命题是真命题的是 ( )
A. |
B. |
C. |
D. |
设向量 与
与 的夹角为
的夹角为 ,定义
,定义 与
与 的“向量积”:
的“向量积”: 是一个向量,它的模
是一个向量,它的模 ,若
,若 ,则
,则
 ( )
( )
A. |
B.2 | C. |
D.4 |
 中,
中, 、
、 、C对应边分别为
、C对应边分别为 、
、 、
、 .若
.若 ,
, ,
, ,且此三角形有两解,则
,且此三角形有两解,则 的取值范围为 ( )
的取值范围为 ( )
A. |
B. |
C. |
D. |
某同学对函数 进行研究后,得出以下五个结论:①函数
进行研究后,得出以下五个结论:①函数 的图象是中心对称图形;②对任意实数
的图象是中心对称图形;②对任意实数 ,
, 均成立;③函数
均成立;③函数 的图象与
的图象与 轴有无穷多个公共点,且任意相邻两点的距离相等;④函数
轴有无穷多个公共点,且任意相邻两点的距离相等;④函数 的图象与直线
的图象与直线 有无穷多个公共点,且任意相邻两点的距离相等;⑤当常数
有无穷多个公共点,且任意相邻两点的距离相等;⑤当常数 满足
满足 时,函数
时,函数 的图象与直线
的图象与直线 有且仅有一个公共点。其中所有正确结论的序号是 ( )
有且仅有一个公共点。其中所有正确结论的序号是 ( )
| A.①②④ | B.①②③④ | C.①②④⑤ | D.①②③④⑤ |
在直角梯形ABCD中, ,动点P在以点C为圆心,且与直线BD相切的圆内运动,设
,动点P在以点C为圆心,且与直线BD相切的圆内运动,设 ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A. |
B. |
C. |
D. |
若长度为定值的线段AB的两端点分别在x轴正半轴和y轴正半轴上移动,O为坐标原点,则 的重心、内心、外心、垂心的轨迹都不可能是 ( )
的重心、内心、外心、垂心的轨迹都不可能是 ( )
| A.点 | B.线段 | C.圆弧 | D.抛物线的一部分 |
已知a,b,c为△ABC的三个内角A,B,C的对 边,向量m=(
边,向量m=( ),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____
),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____
已知函数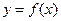 是定义在
是定义在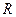 上的增函数,函数
上的增函数,函数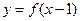 的图象关于点
的图象关于点 (1 , 0)对称,若对任意的
(1 , 0)对称,若对任意的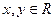 ,不等式
,不等式 恒成立,则当
恒成立,则当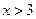 时,
时,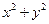 的取值范围是____▲_____
的取值范围是____▲_____
观察下列几个三角恒等式:
①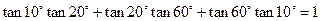 ;
;
②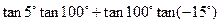
 ;
;
③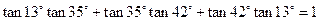 .
.
一般地,若 都有意义,你从这三个恒等式中猜想得到的一个结论为 ▲
都有意义,你从这三个恒等式中猜想得到的一个结论为 ▲
如图,已知 是椭圆
是椭圆
 的左、右焦点, 点
的左、右焦点, 点 在椭圆
在椭圆 上,线段
上,线段 与圆
与圆 相切于点
相切于点 ,且点
,且点 为线段
为线段 的中点,则椭圆
的中点,则椭圆 的离心率为 ▲ .
的离心率为 ▲ .
已知对任意平面向量 =(x,y),把
=(x,y),把 绕其起
绕其起 点沿逆时针方向旋转
点沿逆时针方向旋转 角得到向量
角得到向量 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转 角得到点P. 设平面内曲线C上的每一点绕原点沿逆时针方向旋转
角得到点P. 设平面内曲线C上的每一点绕原点沿逆时针方向旋转 后得到点的轨迹是曲线
后得到点的轨迹是曲线 ,则原来曲线C的方程是____▲_____
,则原来曲线C的方程是____▲_____
已知:函数
 的最大值为
的最大值为 ,最小正周期为
,最小正周期为 .
.
(Ⅰ)求: 的解析式;
的解析式;
(Ⅱ)若 的三条边为
的三条边为 ,
, ,
, ,满足
,满足 ,
, 边所对的角为
边所对的角为 .求:角
.求:角 的取值范围及函数
的取值范围及函数 的值域.
的值域.
已知函数 ,
,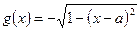 ,
,
(Ⅰ)当 时,若
时,若 在
在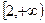 上单调递增,求
上单调递增,求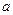 的取值范围;
的取值范围;
(Ⅱ)求满足下列条件的所有实数对 :当
:当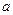 是整数时,存在
是整数时,存在 ,使得
,使得 是
是 的最大值,
的最大值, 是
是 的最小值;
的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对 ,试构造一个定义在
,试构造一个定义在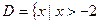 ,且
,且 上的函数
上的函数 ,使当
,使当 时,
时, ,当
,当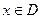 时,
时, 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以 为首项的等差数列。
为首项的等差数列。
(本小题满分14分)
椭圆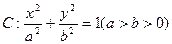 过点P
过点P ,且离心率为
,且离心率为 ,F为椭圆的右焦点,
,F为椭圆的右焦点, 、
、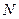 两点在椭圆
两点在椭圆 上,且
上,且 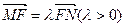 ,定点
,定点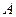 (-4,0).
(-4,0).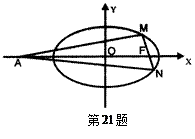
(Ⅰ)求椭圆C的方程;
(Ⅱ)当 时 ,问:MN与AF是否垂直;并证明你的结论.
时 ,问:MN与AF是否垂直;并证明你的结论.
(Ⅲ)当 、
、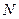 两点在
两点在 上运动,且
上运动,且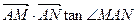 =6
=6 时
时 , 求直线MN的方程.
, 求直线MN的方程.
 )+sinα=
)+sinα= ( )
( )

 是函数
是函数
 的导函数,将
的导函数,将 和
和 的图象画在同一个直角坐标系中,不可能正确的是 ( )
的图象画在同一个直角坐标系中,不可能正确的是 ( )

 的零点个
的零点个 为三个非零向量,且
为三个非零向量,且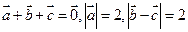 ,则
,则 的最大值是____▲_____.
的最大值是____▲_____. ,
, ,设
,设 ,且函数
,且函数 的零点均在区间
的零点均在区间 内,则
内,则 的最小值为____▲_____.
的最小值为____▲_____.
 ,
, 时,求
时,求 ;
; 的实数
的实数 的取值范围。
的取值范围。 分15分)已知函数
分15分)已知函数 在
在 上为增函数,且
上为增函数,且 ,
,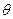 为常数,
为常数,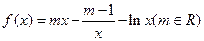 .
.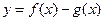 在
在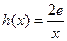 ,若在
,若在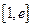 上至少存在一个
上至少存在一个 ,使得
,使得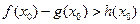 成立,求的m取值范围.
成立,求的m取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号