[广东]2011—2012学年上期广东省潮汕名校高三期中理科数学试卷
设全集U是实数集R,M={x|x2> 4},N={x|x≥3或x<1}都是U的子集,则图中阴影部分所表示的集合是( )
| A.{x|-2≤x<1} | B.{x|-2≤x≤2} | C.{x|1<x≤2} | D.{x|x<2} |
下列命题中的假命题是( )
A. |
B.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
C. |
D.“x<2”是“|x|<2”的充分非必要条件 |
物体A以速度v=3t 2+1(m/s)在一直线l上运动,物体B在直线l上,且在物体A的正前方5 m处,同时以v=10t(m/s)的速度与A同向运动,出发后物体A追上物体B所用的时间t(s)为 ( )
| A.3 | B.4 | C.5 | D.6 |
命题p:方程 有一正根和一负根.命题q:函数
有一正根和一负根.命题q:函数 轴无公共点.若命题“
轴无公共点.若命题“ ”为真命题,而命题“
”为真命题,而命题“ ”为假命题,则实数
”为假命题,则实数 的取值范围是 .
的取值范围是 .
在一条公路上每隔10公里有一个仓库,共有5个仓库.一号仓库存有10吨货物,二号仓库存有20吨货物,五号仓库存有40吨货物,其余两个仓库是空的.现在要把所有的货物集中存放在一个仓库里,若每吨货物运输1公里需要0.5元运输费,则最少需要的运费是 元 
如图,点A,B是单位圆上的两点,A,B点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为( ,
, ),记∠COA=α.
),记∠COA=α.
(1)求 的值;
的值;
(2)求|BC|2的值.
已 知不等式
知不等式 的解集为A,函数
的解集为A,函数 的定义域为B.
的定义域为B.
(Ⅰ)若
 ,求
,求 的取值范围;
的取值范围;
(Ⅱ)证明:函数 的图象关于原点对称。
的图象关于原点对称。
设函数 。
。
(1)求函数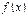 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)若 ,是否存在实数m,使函数
,是否存在实数m,使函数 的值域恰为
的值域恰为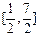 ?若存在,请求出m的
?若存在,请求出m的
取值;若不存在,请说明理由。
某工厂生产某种产品,已知该产品的月生产量 (吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-0.2x2,且生产x吨的成本为
(吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-0.2x2,且生产x吨的成本为 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(注:利润=收入─成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(注:利润=收入─成本)
已知函数: .
.
(1)证明: +
+ +2=0对定义域内的所有
+2=0对定义域内的所有 都成立;
都成立;
(2)当 的定义域为[
的定义域为[ +
+ ,
, +1]时,求证:
+1]时,求证: 的值域为[-3,
的值域为[-3, -2];
-2];
(3)若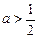 ,函数
,函数 =x2+|(x-
=x2+|(x- )
)  | ,求
| ,求 的最小值
的最小值
 的值为( )
的值为( )



 ,π),sinα=
,π),sinα= ,则tan(α+
,则tan(α+ )等于( )
)等于( )
 ,满足
,满足 的函数
的函数 可以
可以
 在区间
在区间 内的图象是 ( )
内的图象是 ( )

 没有零点,则
没有零点,则 的取值范围为( )
的取值范围为( )



 ,则
,则 的最小值为
的最小值为 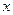 的不等式
的不等式 的解集为
的解集为 ,则实数
,则实数 的值为 .
的值为 . ,则
,则 .
. 的定义域是
的定义域是 (
( 为整数),值域是
为整数),值域是 ,则满
,则满 共有_________个
共有_________个 .
. 的单调区间;
的单调区间; 的图像在点
的图像在点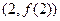 处的切线的倾斜角为
处的切线的倾斜角为 ,问:
,问: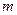 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的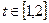 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值? 时,设函数
时,设函数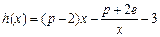 ,若在区间
,若在区间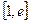 上至少存在
上至少存在 一个
一个 ,
, 成立,试求实数
成立,试求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号