【八年级下册】全国重点高中提前招生单元过关(十二)
如图是某函数的图象,则下列结论中正确的是( )

| A. |
当 时, 的取值是 |
B. |
当 时, 的取值是 |
| C. |
当 时,函数值 最大 |
D. |
当 时, 随 的增大而增大 |
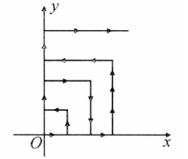
如图,一个粒子在第一象限内及 轴上运动,在第一分钟内它从原点运动到 ,而后它接着按图所示在 轴, 轴平行的方向来回运动且每分钟移动 个单位长度,那么在 分钟这一时刻,这个粒子所处的位置是( )
| A. |
|
B. |
|
C. |
|
D. |
|
“龟兔赛跑”讲述了这样的故事:龟兔同时出发,沿直线向同一目标奔跑,领先的兔子看着缓慢爬行的乌龟,骄傲起来,眯了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晩,乌龟还是先到达了终点….用 分别表示乌龟和兔子所行的路程, 为时间,则下列各图象与故事情节相吻合的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,某天,学校研究性学习小组的同学从 时起骑自行车外出调查, 时回学校,小组离开学校的距离与时间的关系可用图中的曲线表示,根据这个曲线图,下列说法错误的是( )

| A. |
在离校最远的地方调查的时间是 时 |
| B. |
第一次调查 时开始,历时 |
| C. |
中午 时休息的地方离校 |
| D. |
返校的速度最慢 |
已知如图a,点 是 中点,点 在 上,动点 以每秒 的速度沿图a的边线运动,运动路径为 ,相应的 的面积 关于运动的时间 图像如图b,若 ,则下列四个结论中正确的个数有( )
①图 中的 长是 ;②图b中的 点表示第 时 的值为 ;
③图a中的 长是 ;④图b中的 点表示第 时, 的值为 .

| A. |
个 |
B. |
个 |
C. |
个 |
D. |
个 |
小车匀速通过隧道时,火车在隧道内的长度 与火车行驶时间 之间的关系用图像描述如图所示,有下列结论:
①火车的长度为 ;②火车的速度为 ;③火车整体都在隧道内的时间为 ;④隧道长度为 .
其中正确的结论是_____.(把你认为正确结论的序号都填上)

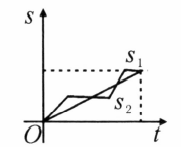
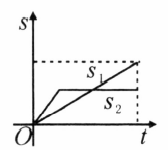
甲、乙两人以相同路线前往离学校 的地方参加植树活动,图中 , 分别表示甲、乙两人前往目的地所行驶的路程 随时间 变化的函数图像,则乙每分钟比甲少行驶_____.

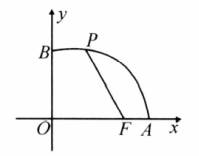
如图,已知点 的坐标为 ,点 分别是某函数图像与 轴, 轴的交点,点 是此图像上的一动点.设点 的横坐标为 的长为 ,且 与 之间满足关系: ,给出以下四个结论:① ;② ;③ ;④ .
其中正确结论的序号是_____.
如果记 ,同理 表示当 时 的值,即 ,同理 表示当 时 的值,即 ,……,那么 _____.(结果用含有 的代数式表示, 为正整数)
已知函数 ,其中 表示 时对应的函数值,即 .
(1)求 ;
(2)计算: 的值;
(3)如果 ,试求 的值.
某单位计划派若干名员工参加电脑培训,现从两家电脑公司了解到,同样的培训条件,每名学员的培训费都报价为 元,甲公司的优惠条件是:一名学员按报价收费,其余学员每人优惠 ;乙公司的优惠条件是:每名学员优惠20%.
(1)分别写出甲、乙两公司总收费 (元)关于学员人数 (人)的函数解析式;
(2)讨论该单位在哪家公司的培训总费用较低.
某景区的旅游线路如图①,其中 为人口, 为风景点, 为三岔路的交汇点。图①中所给数据为相应两点间的路程(单位: ).甲游客以一定的速度沿线路“ ”步行游览,在每个景点,逗留的时间相同,当他回到 处时,共用去 .甲步行的路程 与游览时间 之间的部分函数图像如图②所示.
(1)求甲在每个景点逗留的时间,并补全图像;
(2)求 两点间的路程;
(3)乙游客与甲游客同时从 处出发,打算游完三个景点后回到 处,两人相约先到者在 处等候,等候时间不超过 .如果乙的步行速度为 ,在每个景点逗留的时间与甲相同,他们的约定能否实现?请说明理由.

阅读下面的材料:
例1:求函数 的反函数;
解:由 ,可得 ,所以原函数 的反函数是 .
例2求函数 的反函数.
解:由 ,可得 ,所以原函数 的反函数是 .
以上两例中,在相应的条件下,一个原函数有反函数时,原函数中自变量 的取值范围就是它的反函数中函数值 的取值范围,原函数中函数值 的取值范围就是它的反函数中自变量 的取值范围,通过以上内容完成下面任务.
(1)求函数 的反函数;
(2)函数 的反函数的函数值的取值范围为_____;
| A. |
|
B. |
|
C. |
|
D. |
|
(3)下列函数中反函数是它本身的是_____(填序号即可).
① ;② ;③ ;④ ;⑤





 粤公网安备 44130202000953号
粤公网安备 44130202000953号