2022年上海市中考数学试卷
我们在外卖平台点单时会有点餐用的钱和外卖费 元,我们计算了点单的总额和不计算外卖费的总额的数据,则两种情况计算出的数据一样的是( )
| A. |
平均数 |
B. |
中位数 |
C. |
众数 |
D. |
方差 |
下列说法正确的是( )
| A. |
命题一定有逆命题 |
| B. |
所有的定理一定有逆定理 |
| C. |
真命题的逆命题一定是真命题 |
| D. |
假命题的逆命题一定是假命题 |
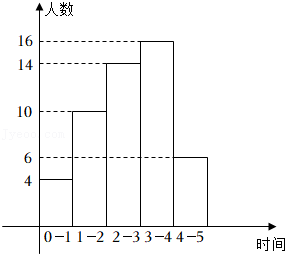
为了解学生的阅读情况,对某校六年级部分学生的阅读情况展开调查,并列出了相应的频数分布直方图(如图所示)(每组数据含最小值,不含最大值)( 小时 人, 小时 人, 小时 人, 小时 人, 小时 人),若共有 名学生,则该学校六年级学生阅读时间不低于 小时的人数是_____.
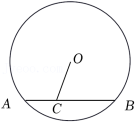
定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为 的等腰直角三角形,当等弦圆最大时,这个圆的半径为_____.
一个一次函数的截距为 ,且经过点 .
(1)求这个一次函数的解析式;
(2)点 在某个反比例函数上,点 横坐标为 ,将点 向上平移 个单位得到点 ,求 的值.
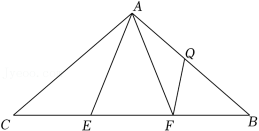
我们经常会采用不同方法对某物体进行测量,请测量下列灯杆 的长.
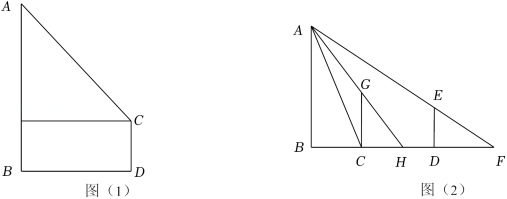
(1)如图(1)所示,将一个测角仪放置在距离灯杆 底部 米的点 处,测角仪高为 米,从 点测得 点的仰角为 ,求灯杆 的高度.(用含 的代数式表示)
(2)我国古代数学家赵爽利用影子对物体进行测量的方法,在至今仍有借鉴意义.如图(2)所示,现将一高度为 米的木杆 放在灯杆 前,测得其影长 为 米,再将木杆沿着 方向移动 米至 的位置,此时测得其影长 为 米,求灯杆 的高度.
在平面直角坐标系 中,抛物线 过点 .
(1)求抛物线的解析式;
(2)平移抛物线,平移后的顶点为 .
ⅰ.如果 ,设直线 ,在这条直线的右侧原抛物线和新抛物线均呈上升趋势,求k的取值范围;
ⅱ.点 在原抛物线上,新抛物线交 轴于点 ,且 ,求点 的坐标.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号