2022年广东省广州市中考数学试卷

如图是一个几何体的侧面展开图，这个几何体可以是（　　）

下列图形中，是中心对称图形的是（　　）

代数式 $\frac{1}{\sqrt{x+1}}$有意义时，x应满足的条件为（　　）

点 $（3,﹣5）$在正比例函数 $y＝kx（k\ne 0）$的图象上，则 $k$的值为（　　）

下列运算正确的是（　　）

如图，抛物线 $y＝a{x}^2+bx+c（a\ne 0）$的对称轴为 $x=-2$，下列结论正确的是（　　）

实数a，b在数轴上的位置如图所示，则（　　）

为了疫情防控，某小区需要从甲、乙、丙、丁4名志愿者中随机抽取2名负责该小区入口处的测温工作，则甲被抽中的概率是（　　）

如图，正方形 $ABCD$的面积为3，点E在边CD上，且 $CE＝1$， $\angle ABE$的平分线交AD于点F，点M，N分别是 $BE，BF$的中点，则 $MN$的长为（　　）

如图，用若干根相同的小木棒拼成图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒，则 $n$的值为（　　）

在甲、乙两位射击运动员的10次考核成绩中，两人的考核成绩的平均数相同，方差分别为 ${S_{甲}}^2＝1.45$， ${S_{乙}}^2＝0.85$，则考核成绩更为稳定的运动员是 　 　．（填“甲”、“乙”中的一个）．

分解因式： $3a^2﹣21ab$＝　 　．

如图，在 $▱ABCD$中， $AD＝10$，对角线AC与BD相交于点O， $AC+BD＝22$，则△BOC的周长为 　 　．

分式方程 $\frac{3}{2x}=\frac{2}{x+1}$的解是 　 　．

如图，在 $△ABC$中， $AB＝AC$，点O在边AC上，以O为圆心，4为半径的圆恰好过点C，且与边AB相切于点D，交BC于点E，则劣弧 $\stackrel{̂}{\mathit{DE}}$的长是 　 　．（结果保留π）

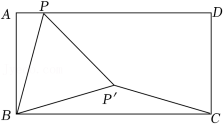
如图，在矩形 $ABCD$中， $BC＝2AB$，点P为边AD上的一个动点，线段BP绕点B顺时针旋转60°得到线段 $BP\prime$，连接 $PP\prime ,CP\prime$．当点P′落在边BC上时， $\angle PP\prime C$的度数为 　 　；当线段 $CP\prime$的长度最小时， $\angle PP\prime C$的度数为 　 　．

解不等式： $3x﹣2＜4$．

如图，点D，E在△ABC的边BC上， $\angle B＝\angle C,BD＝CE$，求证： $△ABD≌△ACE$．

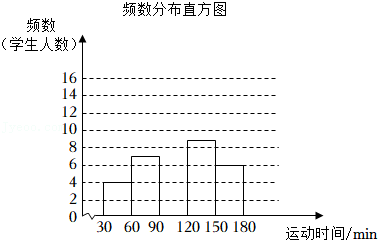
某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查，根据调查结果绘制了如下不完整的频数分布表和频数分布直方图．

频数分布表

请根据图表中的信息解答下列问题：

（1）频数分布表中的a＝　 　，b＝　 　，n＝　 　；

（2）请补全频数分布直方图；

（3）若该校九年级共有480名学生，试估计该校九年级学生平均每天体育运动时间不低于120min的学生人数．

某燃气公司计划在地下修建一个容积为 $V$（ $V$为定值，单位： $m^3$）的圆柱形天然气储存室，储存室的底面积 $S$（单位： $m^2$）与其深度 $d$（单位： $m$）是反比例函数关系，它的图象如图所示．

（1）求储存室的容积V的值；

（2）受地形条件限制，储存室的深度d需要满足 $16\le d\le 25$，求储存室的底面积S的取值范围．

已知 $T=（a+3b{）}^2+（2a+3b）（2a﹣3b）+a^2$．

（1）化简 $T$；

（2）若关于 $x$的方程 $x^2+2ax﹣ab+1＝0$有两个相等的实数根，求 $T$的值．

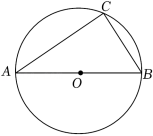
如图，AB是⊙O的直径，点C在⊙O上，且 $AC＝8,BC＝6$．

（1）尺规作图：过点O作AC的垂线，交劣弧 $\stackrel{̂}{\mathit{AC}}$于点D，连接CD（保留作图痕迹，不写作法）；

（2）在（1）所作的图形中，求点O到AC的距离及 $\sin \angle ACD$的值．

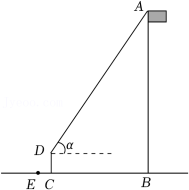
某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度．如图，在某一时刻，旗杆AB的影子为BC，与此同时在C处立一根标杆CD，标杆CD的影子为CE， $CD＝1.6m,BC＝5CD$．

（1）求 $BC$的长；

（2）从条件①、条件②这两个条件中选择一个作为已知，求旗杆AB的高度．

条件①： $CE＝1.0m$；条件②：从D处看旗杆顶部A的仰角 $\alpha$为 $54.46°$．

注：如果选择条件①和条件②分别作答，按第一个解答计分．

参考数据： $\sin 54.46°\approx 0.81,\cos 54.46°\approx 0.58,\tan 54.46°\approx 1.40$．

已知直线 $l：y＝kx+b$经过点 $（0,7）$和点 $（1,6）$．

（1）求直线 $l$的解析式；

（2）若点 $P（m,n）$在直线l上，以P为顶点的抛物线G过点 $（0,﹣3）$，且开口向下．

①求m的取值范围；

②设抛物线G与直线l的另一个交点为Q，当点Q向左平移1个单位长度后得到的点 $Q\prime$也在G上时，求G在 $\frac{4m}{5}\le x\le \frac{4m}{5}+1$的图象的最高点的坐标．

如图，在菱形 $ABCD$中， $\angle BAD＝120°$， $AB＝6$，连接 $BD$．

（1）求 $BD$的长；

（2）点E为线段 $BD$上一动点（不与点B，D重合），点 $F$在边 $AD$上，且 $BE=\sqrt{3}DF$．

①当 $CE\perp AB$时，求四边形 $ABEF$的面积；

②当四边形 $ABEF$的面积取得最小值时， $CE+\sqrt{3}CF$的值是否也最小？如果是，求 $CE+\sqrt{3}CF$的最小值；如果不是，请说明理由．