2020年重庆市中考数学试卷(b卷)
小明准备用 元钱购买作业本和签字笔.已知每个作业本6元,每支签字笔2.2元,小明买了7支签字笔,他最多还可以买的作业本个数为( )
| A. |
5 |
B. |
4 |
C. |
3 |
D. |
2 |
下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,…,按此规律排列下去,第⑥个图形中实心圆点的个数为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,垂直于水平面的 信号塔 AB建在垂直于水平面的悬崖边 B点处,某测量员从山脚 C点出发沿水平方向前行78米到 D点(点 A, B, C在同一直线上),再沿斜坡 方向前行78米到 E点(点 A, B, C, D, E在同一平面内),在点 E处测得 信号塔顶端 A的仰角为43°,悬崖 BC的高为144.5米,斜坡 DE的坡度(或坡比) ,则信号塔 AB的高度约为( )
(参考数据: , , )

| A. |
23米 |
B. |
24米 |
C. |
24.5米 |
D. |
25米 |
若关于 x的一元一次不等式组 的解集为 ,且关于 y的分式方程 有非负整数解,则符合条件的所有整数 a的和为( )
| A. |
|
B. |
﹣2 |
C. |
﹣3 |
D. |
0 |
如图,在 中, , , ,将 沿直线 AC翻折至 所在的平面内,得 .过点 A作 ,使 ,与 的延长线交于点 E,连接 BE,则线段 BE的长为( )

| A. |
|
B. |
3 |
C. |
|
D. |
4 |
如图,在平面直角坐标系中,矩形 ABCD的顶点 A, C分别在 x轴, y轴的正半轴上,点 , ,若反比例函数 的图象经过点 B,则 k的值为( )

| A. |
|
B. |
8 |
C. |
10 |
D. |
|
盒子里有3张形状、大小、质地完全相同的卡片,上面分别标着数字1,2,3,从中随机抽出1张后不放回,再随机抽出1张,则两次抽出的卡片上的数字之和为奇数的概率是 .
如图,在菱形 中,对角线 交于点O, , ,以点O为圆心, 长为半径画弧,分别与菱形的边相交,则图中阴影部分的面积为 .(结果保留π)

周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的 继续骑行,经过一段时间,甲先到达B地,乙一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(单位:米)与乙骑行的时间x(单位:分钟)之间的关系如图所示,则乙比甲晚 分钟到达B地.

为刺激顾客到实体店消费,某商场决定在星期六开展促销活动.活动方案如下:在商场收银台旁放置一个不透明的箱子,箱子里有红、黄、绿三种颜色的球各一个(除颜色外大小、形状、质地等完全相同),顾客购买的商品达到一定金额可获得一次摸球机会,摸中红、黄、绿三种颜色的球可分别返还现金50元、30元、10元.商场分三个时段统计摸球次数和返现金额,汇总统计结果为:第二时段摸到红球次数为第一时段的3倍,摸到黄球次数为第一时段的2倍,摸到绿球次数为第一时段的4倍;第三时段摸到红球次数与第一时段相同,摸到黄球次数为第一时段的4倍,摸到绿球次数为第一时段的2倍,三个时段返现总金额为2510元,第三时段返现金额比第一时段多420元,则第二时段返现金额为 元.
每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据统计、整理如下:
八年级抽取的学生的竞赛成绩:
4,4,6,6,6,6,7,7,7,8,8,8,8,8,8,9,9,9,10,10.
七、八年级抽取的学生的竞赛成绩统计表
年级 |
七年级 |
八年级 |
平均数 |
7.4 |
7.4 |
中位数 |
a |
b |
众数 |
7 |
c |
合格率 |
85% |
90% |
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数;
(3)根据以上数据分析,从一个方面评价两个年级“国家安全法”知识竞赛的学生成绩谁更优异.

在数的学习过程中,我们总会对其中一些具有某种特性的数充满好奇,如学习自然数时,我们发现一种特殊的自然数﹣﹣“好数”.
定义:对于三位自然数n,各位数字都不为0,且百位数字与十位数字之和恰好能被个位数字整除,则称这个自然数n为“好数”.
例如: 是“好数”,因为4,2,6都不为0,且 ,6能被6整除;
643不是“好数”,因为 ,10不能被3整除.
(1)判断 , 是否是“好数”?并说明理由;
(2)求出百位数字比十位数字大5的所有“好数”的个数,并说明理由.
探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数 的图象并探究该函数的性质.
x |
… |
﹣4 |
﹣3 |
﹣2 |
﹣1 |
0 |
1 |
2 |
3 |
4 |
… |
y |
… |
|
a |
﹣2 |
﹣4 |
b |
﹣4 |
﹣2 |
|
|
… |
(1)列表,写出表中 , 的值: , ;
描点、连线,在所给的平面直角坐标系中画出该函数的图象.
(2)观察函数图象,判断下列关于函数性质的结论是否正确(在答题卡相应位置正确的用“√”作答,错误的用“×”作答):
①函数 的图象关于y轴对称;
②当 时,函数 有最小值,最小值为 ;
③在自变量的取值范围内函数y的值随自变量x的增大而减小.
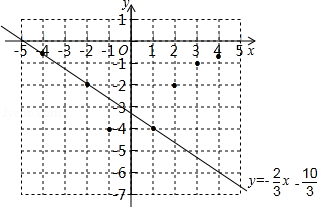
(3)已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.
为响应“把中国人的饭碗牢牢端在自己手中”的号召,确保粮食安全,优选品种,提高产量,某农业科技小组对 , 两个玉米品种进行实验种植对比研究.去年 、 两个品种各种植了10亩.收获后 、 两个品种的售价均为 元/kg,且 品种的平均亩产量比A品种高100千克, 、 两个品种全部售出后总收入为 元.
(1)求 、 两个品种去年平均亩产量分别是多少千克?
(2)今年,科技小组优化了玉米的种植方法,在保持去年种植面积不变的情况下,预计A、B两个品种平均亩产量将在去年的基础上分别增加 和 .由于B品种深受市场欢迎,预计每千克售价将在去年的基础上上涨 ,而A品种的售价保持不变, 、 两个品种全部售出后总收入将增加 .求a的值.
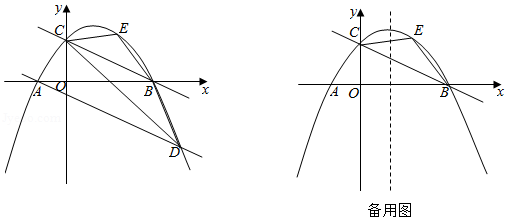
如图,在平面直角坐标系中,抛物线 与 轴交于点 ,与x轴交于 两点(点 在点 的左侧),且 点坐标为 ,直线 的解析式为 .
(1)求抛物线的解析式;
(2)过点 作 ,交抛物线于点D,点E为直线 上方抛物线上一动点,连接CE,EB,BD,DC.求四边形BECD面积的最大值及相应点E的坐标;
(3)将抛物线 向左平移 个单位,已知点 为抛物线 的对称轴上一动点,点N为平移后的抛物线上一动点.在(2)中,当四边形 的面积最大时,是否存在以 为顶点的四边形为平行四边形?若存在,直接写出点N的坐标;若不存在,请说明理由.
 长方体
长方体 圆柱体
圆柱体 球体
球体 圆锥体
圆锥体



 粤公网安备 44130202000953号
粤公网安备 44130202000953号