2020年山东省济宁市中考数学试卷
一条船从海岛 出发,以15海里 时的速度向正北航行,2小时后到达海岛 处.灯塔 在海岛 的北偏西 方向上,在海岛 的北偏西 方向上.则海岛 到灯塔 的距离是
A.15海里B.20海里C.30海里D.60海里
下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位: 的平均数和方差,要从中选择一名成绩较高且发挥稳定的运动员参加决赛,最合适的运动员是
甲 |
乙 |
丙 |
丁 |
|
平均数 |
376 |
350 |
376 |
350 |
方差 |
12.5 |
13.5 |
2.4 |
5.4 |
A.甲B.乙C.丙D.丁
数形结合是解决数学问题常用的思想方法.如图,直线 和直线 相交于点 ,根据图象可知,方程 的解是
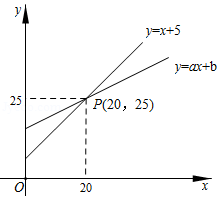
A. B. C. D.
小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案(如图所示),每个图案中他只在最下面的正方体上写“心”字,寓意“不忘初心”.其中第(1)个图案中有1个正方体,第(2)个图案中有3个正方体,第(3)个图案中有6个正方体, 按照此规律,从第 个图案所需正方体中随机抽取一个正方体,抽到带“心”字正方体的概率是

A. B. C. D.
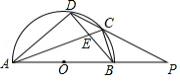
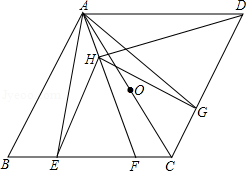
如图,在四边形 中,以 为直径的半圆 经过点 , . 与 相交于点 , ,分别延长 , 相交于点 , , .则 的长是 .
某校举行了"防溺水"知识竞赛.八年级两个班各选派10名同学参加预赛,依据各参赛选手的成绩(均为整数)绘制了统计表和折线统计图(如图所示).
班级 |
八(1)班 |
八(2)班 |
最高分 |
100 |
99 |
众数 |
|
98 |
中位数 |
96 |
|
平均数 |
|
94.8 |

(1)统计表中, , , ;
(2)若从两个班的预赛选手中选四名学生参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在成绩为98分的学生中任选两个,求另外两个决赛名额落在不同班级的概率.
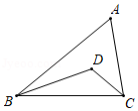
如图,在 中, ,点 在 上.
(1)求作: ,使点 在 上,且 ;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若 .求证: .

在 中, 边的长为 , 边上的高为 , 的面积为2.
(1) 关于 的函数关系式是 , 的取值范围是 ;
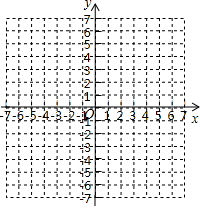
(2)在平面直角坐标系中画出该函数图象;
(3)将直线 向上平移 个单位长度后与上述函数图象有且只有一个交点,请求出此时 的值.
为加快复工复产,某企业需运输一批物资.据调查得知,2辆大货车与3辆小货车一次可以运输600箱;5辆大货车与6辆小货车一次可以运输1350箱.
(1)求1辆大货车和1辆小货车一次可以分别运输多少箱物资;
(2)计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元.请你列出所有运输方案,并指出哪种方案所需费用最少.最少费用是多少?
我们把方程 称为圆心为 、半径长为 的圆的标准方程.例如,圆心为 、半径长为3的圆的标准方程是 .在平面直角坐标系中, 与轴交于点 , ,且点 的坐标为 ,与 轴相切于点 ,过点 , , 的抛物线的顶点为 .
(1)求 的标准方程;
(2)试判断直线 与 的位置关系,并说明理由.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号