2018年江苏省扬州市中考数学试卷
下列说法正确的是
A.一组数据2,2,3,4,这组数据的中位数是2
B.了解一批灯泡的使用寿命的情况,适合抽样调查
C.小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D.某日最高气温是 ,最低气温是 ,则该日气温的极差是
在平面直角坐标系的第二象限内有一点 ,点 到 轴的距离为3,到 轴的距离为4,则点 的坐标是
A. B. C. D.
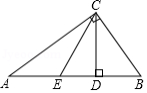
如图,点 在线段 上,在 的同侧作等腰 和等腰 , 与 、 分别交于点 , .对于下列结论:
① ;② ;③ .其中正确的是

A.①②③B.①C.①②D.②③
江苏省第十九届运动会将于2018年9月在扬州举行开幕式,某校为了了解学生“最喜爱的省运会项目”的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、“羽毛球”、“自行车”、“游泳”和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的省运会项目的人数调查统计表
最喜爱的项目 |
人数 |
篮球 |
20 |
羽毛球 |
9 |
自行车 |
10 |
游泳 |
|
其他 |
|
合计 |
根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 , .
(2)扇形统计图中“自行车”对应的扇形的圆心角为 .
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.

4张相同的卡片分别写着数字 、 、4、6,将卡片的背面朝上,并洗匀.
(1)从中任意抽取1张,抽到的数字是奇数的概率是 ;
(2)从中任意抽取1张,并将所取卡片上的数字记作一次函数 中的 ;再从余下的卡片中任意抽取1张,并将所取卡片上的数字记作一次函数 中的 .利用画树状图或列表的方法,求这个一次函数的图象经过第一、二、四象限的概率.
京沪铁路是我国东部沿海地区纵贯南北的交通大动脉,全长 ,是我国最繁忙的铁路干线之一.如果从北京到上海的客车速度是货车速度的2倍,客车比货车少用 ,那么货车的速度是多少?(精确到
如图,在平行四边形 中, ,点 是 的中点,连接 并延长,交 的延长线于点 ,连接 .
(1)求证:四边形 是菱形;
(2)若 , ,求菱形 的面积.

如图,在 中, , 于点 , 于点 ,以点 为圆心, 为半径作半圆,交 于点 .
(1)求证: 是 的切线;
(2)若点 是 的中点, ,求图中阴影部分的面积;
(3)在(2)的条件下,点 是 边上的动点,当 取最小值时,直接写出 的长.

“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元 件,每天销售 (件 与销售单价 (元 之间存在一次函数关系,如图所示.
(1)求 与 之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.

问题呈现
如图1,在边长为1的正方形网格中,连接格点 , 和 , , 和 相交于点 ,求 的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点 , ,可得 ,则 ,连接 ,那么 就变换到 中.
问题解决
(1)直接写出图1中 的值为 2 ;
(2)如图2,在边长为1的正方形网格中, 与 相交于点 ,求 的值;
思维拓展
(3)如图3, , ,点 在 上,且 ,延长 到 ,使 ,连接 交 的延长线于点 ,用上述方法构造网格求 的度数.


 B.
B. C.
C. D.
D.




 粤公网安备 44130202000953号
粤公网安备 44130202000953号