2018年四川省泸州市中考数学试卷
某校对部分参加夏令营的中学生的年龄(单位:岁)进行统计,结果如下表:
年龄 |
13 |
14 |
15 |
16 |
17 |
人数 |
1 |
2 |
2 |
3 |
1 |
则这些学生年龄的众数和中位数分别是
A.16,15B.16,14C.15,15D.14,15
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为 ,较短直角边长为 .若 ,大正方形的面积为25,则小正方形的边长为

A.9B.6C.4D.3
在平面直角坐标系内,以原点 为圆心,1为半径作圆,点 在直线 上运动,过点 作该圆的一条切线,切点为 ,则 的最小值为
A.3B.2C. D.
已知二次函数 (其中 是自变量),当 时, 随 的增大而增大,且 时, 的最大值为9,则 的值为
A.1或 B. 或 C. D.1
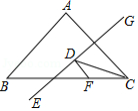
如图,等腰 的底边 ,面积为120,点 在边 上,且 , 是腰 的垂直平分线,若点 在 上运动,则 周长的最小值为 .
为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求 的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.

某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本乙图书?
如图,甲建筑物 ,乙建筑物 的水平距离 为 ,且乙建筑物的高度是甲建筑物高度的6倍,从 , , 在同一水平线上)点测得 点的仰角为 ,测得 点的仰角为 ,求这两座建筑物顶端 、 间的距离(计算结果用根号表示,不取近似值).

一次函数 的图象经过点 , .
(1)求该一次函数的解析式;
(2)如图,该一次函数的图象与反比例函数 的图象相交于点 , , , ,与 轴交于点 ,且 ,求 的值.

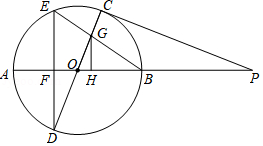
如图,已知 , 是 的直径,过点 作 的切线交 的延长线于点 , 的弦 交 于点 ,且 .
(1)求证: ;
(2)连接 交 于点 ,过点 作 于点 ,若 , ,求 的长.

 B.
B. C.
C. D.
D.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号