2017年四川省南充市中考数学试卷
据统计,参加南充市2016年高中阶段学校招生考试的人数为55354人,这个数用科学记数法表示为
A. B. C. D.
某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:
成绩 分 |
36 |
37 |
38 |
39 |
40 |
人数 人 |
1 |
2 |
1 |
4 |
2 |
下列说法正确的是
A.这10名同学体育成绩的中位数为38分
B.这10名同学体育成绩的平均数为38分
C.这10名同学体育成绩的众数为39分
D.这10名同学体育成绩的方差为2
经过某十字路口的汽车,可直行,也可向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过该十字路口时都直行的概率是 .
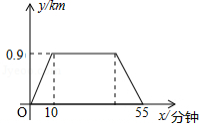
小明从家到图书馆看报然后返回,他离家的距离 与离家的时间 之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 .
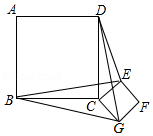
如图,正方形 和正方形 边长分别为 和 ,正方形 绕点 旋转,给出下列结论:① ;② ;③ ,其中正确结论是 (填序号)
在“弘扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“ 国学诵读”、“ 演讲”、“ 课本剧”、“ 书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动 占 ,希望参加活动 占 ,则被调查的总人数为 人,扇形统计图中,希望参加活动 所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动 有多少人?

如图,直线 为常数, 与双曲线 为常数, 的交点为 、 , 轴于点 , , .
(1)求 的值;
(2)点 在 轴上,如果 ,求 点的坐标.

如图, 在 中, ,以 为直径作 交 于点 , 为 的中点, 连接 并延长交 的延长线于点 .
(1) 求证: 是 的切线;
(2) 若 , ,求 直径的长 .

学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人.已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
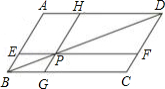
如图,在正方形 中,点 、 分别是边 、 的中点, .
(1)求证: ;
(2)若点 、 分别在射线 、 上同时向右、向上运动,点 运动速度是点 运动速度的2倍, 是否成立(只写结果,不需说明理由)?
(3)正方形 的边长为4, 是正方形 内一点,当 ,求 周长的最小值.


 B .
B . C .
C . D .
D .


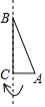


 粤公网安备 44130202000953号
粤公网安备 44130202000953号