2018年湖北省咸宁市中考数学试卷
2017年,咸宁市经济运行总体保持平稳较快增长,全年 约123500000000元,增速在全省17个市州中排名第三,将123500000000用科学记数法表示为
A. B. C. D.
用4个完全相同的小正方体搭成如图所示的几何体,该几何体的

A.主视图和左视图相同B.主视图和俯视图相同
C.左视图和俯视图相同D.三种视图都相同
甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离 (米)与甲出发的时间 (分)之间的关系如图所示,下列结论:
①甲步行的速度为60米 分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米.
其中正确的结论有

A.1个B.2个C.3个D.4个
一个不透明的口袋中有三个完全相同的小球,它们的标号分别为1,2,3.随机摸出一个小球然后放回,再随机摸出一个小球,则两次摸出的小球标号相同的概率是 .
如图,航拍无人机从 处测得一幢建筑物顶部 的仰角为 ,测得底部 的俯角为 ,此时航拍无人机与该建筑物的水平距离 为 ,那么该建筑物的高度 约为 (结果保留整数, .
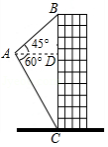
如图,已知 ,点 , 分别在 , 上,且 ,将射线 绕点 逆时针旋转得到 ,旋转角为 且 ,作点 关于直线 的对称点 ,画直线 交 于点 ,连接 , ,有下列结论:
① ;
② 的大小随着 的变化而变化;
③当 时,四边形 为菱形;
④ 面积的最大值为 ;
其中正确的是 .(把你认为正确结论的序号都填上).
已知: .
求作: ,使
(1)如图1,以点 为圆心,任意长为半径画弧,分别交 , 于点 、 ;
(2)如图2,画一条射线 ,以点 为圆心, 长为半径画弧,交 于点 ;
(3)以点 为圆心, 长为半径画弧,与第2步中所画的弧交于点 ;
(4)过点 画射线 ,则 .
根据以上作图步骤,请你证明 .

近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 |
0 |
1 |
2 |
3 |
4 |
5 |
人数 |
11 |
15 |
23 |
28 |
18 |
5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
如图,在平面直角坐标系中,矩形 的顶点 的坐标为 ,直线 与边 , 分别相交于点 , ,函数 的图象过点 .
(1)试说明点 也在函数 的图象上;
(2)将直线 沿 轴的负方向平移得到直线 ,当直线 与函数 的图象仅有一个交点时,求直线 的解析式.

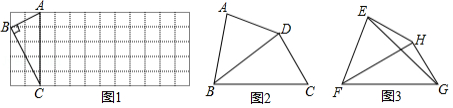
如图,以 的边 为直径的 恰为 的外接圆, 的平分线交 于点 ,过点 作 交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 |
乙种客车 |
|
载客量 (人 辆) |
30 |
42 |
租金 (元 辆) |
300 |
400 |
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆;
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
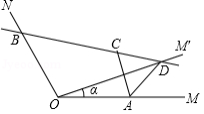
(1)如图1,已知 在正方形网格中,请你只用无刻度的直尺在网格中找到一点 ,使四边形 是以 为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形 中, , ,对角线 平分 .
求证: 是四边形 的“相似对角线”;
(3)如图3,已知 是四边形 的“相似对角线”, ,连接 ,若 的面积为 ,求 的长.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号