2017年湖南省衡阳市中考数学试卷
中国超级计算机神威“太湖之光”,峰值计算速度达每秒12.5亿亿次,为世界首台每秒超10亿亿次运算的计算机,用科学记数法表示12.5亿亿次 秒为 亿次 秒.
A. B. C. D.
下面调查方式中,合适的是
A.调查你所在班级同学的身高,采用抽样调查方式
B.调查湘江的水质情况,采用抽样调查的方式
C.调查 《 总决赛》栏目在我市的收视率,采用普查的方式
D.要了解全市初中学生的业余爱好,采用普查的方式
中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2015年年收入200美元,预计2017年年收入将达到1000美元,设2015年到2017年该地区居民年人均收入平均增长率为 ,可列方程为
A. B.
C. D.
下列命题是假命题的是
A . 不在同一直线上的三点确定一个圆
B . 角平分线上的点到角两边的距离相等
C . 正六边形的内角和是
D . 角的边越大, 角就越大
某班7名同学在“课间一分钟跳绳”比赛中,成绩(单位:个)分别是:150,182,182,180,201,175,181,这组数据的中位数是 181 .
如图,方格图中每个小正方形的边长为1,点 、 、 都是格点.
(1)画出 关于直线 对称的△ ;
(2)写出 的长度.

某校300名学生参加植树活动,要求每人植树 棵,活动结束后随机抽查了20名学生每人的植树量,并分为四类: 类2棵、 类3棵、 类4棵、 类5棵,将各类的人数绘制成不完整的条形统计图(如图所示),回答下列问题:
(1) 类学生有多少人?
(2)估计这300名学生共植树多少棵?

为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为: .唐诗; .宋词; .论语; .三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在 处用高为1.5米的测角仪 ,测得塔顶 的仰角为 ,再向塔身前进10.4米,又测得塔顶 的仰角为 ,求来雁塔的高度.(结果精确到0.1米)

为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额 (元 与骑行时间 (时 之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额 (元 与骑行时间 (时 的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

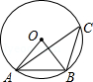
如图,已知 内接于 , 为 的直径, ,交 的延长线于点 .
(1) 为 的中点,连接 ,求证: 是 的切线;
(2)若 ,求 的大小.

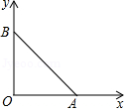
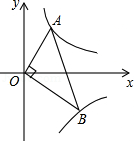
如图, 的顶点 、 分别在 轴, 轴上, ,且 的面积为8.
(1)直接写出 、 两点的坐标;
(2)过点 、 的抛物线 与 轴的另一个交点为点 .
①若 是以 为腰的等腰三角形,求此时抛物线的解析式;
②将抛物线 向下平移4个单位后,恰好与直线 只有一个交点 ,求点 的坐标.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号