2017年贵州省遵义市中考数学试卷
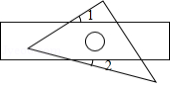
把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是

A. B.
B.
C. D.
D.
我市某连续7天的最高气温为: , , , , , , ,这组数据的平均数和众数分别是
A. , B. , C. , D. ,
如图,抛物线 经过点 ,对称轴 如图所示.则下列结论:① ;② ;③ ;④ ,其中所有正确的结论是
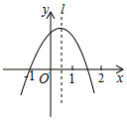
A.①③B.②③C.②④D.②③④
明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:所分的银子共有 两.(注:明代时1斤 两,故有“半斤八两”这个成语)
学校召集留守儿童过端午节,桌上摆有甲、乙两盘粽子,每盘中盛有白粽2个,豆沙粽1个,肉粽1个(粽子外观完全一样).
(1)小明从甲盘中任取一个粽子,取到豆沙粽的概率是 ;
(2)小明在甲盘和乙盘中先后各取了一个粽子,请用树状图或列表法求小明恰好取到两个白粽子的概率.
乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥 和引桥 两部分组成(如图所示),建造前工程师用以下方式做了测量:无人机在 处正上方 处的 点,测得 处的俯角为 (当时 处被小山体阻挡无法观测).无人机飞行到 处正上方的 处时能看到 处,此时测得 处俯角为 .
(1)求主桥 的长度;
(2)若两观察点 、 的连线与水平方向的夹角为 ,求引桥 的长.
(长度均精确到 ,参考数据: , , ,

贵州省是我国首个大数据综合试验区,大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值.为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:

(1)本次参与调查的人数有 人;
(2)关注城市医疗信息的有 人,并补全条形统计图;
(3)扇形统计图中, 部分的圆心角是 度;
(4)说一条你从统计图中获取的信息.
如图, 、 是 的切线, 、 为切点, ,连接 并延长与 交于 点,连接 , .
(1)求证:四边形 是菱形;
(2)若 半径为1,求菱形 的面积.

为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车” 公益活动登陆我市中心城区.某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括 、 两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放 、 两型自行车各50辆,投放成本共计7500元,其中 型车的成本单价比 型车高10元, 、 两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放 辆“小黄车”,乙街区每1000人投放 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求 的值.
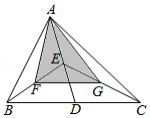
边长为 的正方形 中, 是对角线 上的一个动点(点 与 、 不重合),连接 ,将 绕点 顺时针旋转 到 ,连接 , 与 交于点 , 延长线与 (或 延长线)交于点 .
(1)连接 ,证明: ;
(2)设 , ,试写出 关于 的函数关系式,并求当 为何值时, ;
(3)猜想 与 的数量关系,并证明你的结论.

如图,抛物线 , 、 为常数)与 轴交于 、 两点,与 轴交于 点,直线 的函数关系式为 .
(1)求该抛物线的函数关系式与 点坐标;
(2)已知点 是线段 上的一个动点,过点 作 轴的垂线 分别与直线 和抛物线交于 、 两点,当 为何值时, 恰好是以 为底边的等腰三角形?
(3)在(2)问条件下,当 恰好是以 为底边的等腰三角形时,动点 相应位置记为点 ,将 绕原点 顺时针旋转得到 (旋转角在 到 之间);
.探究:线段 上是否存在定点 不与 、 重合),无论 如何旋转, 始终保持不变.若存在,试求出 点坐标;若不存在,请说明理由;
.试求出此旋转过程中, 的最小值.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号