2018年内蒙古呼和浩特市中考数学试卷
二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长,根据如图,在下列选项中指出白昼时长低于11小时的节气( )

| A. |
惊蛰 |
B. |
小满 |
C. |
立秋 |
D. |
大寒 |
已知一个多边形的内角和为1080°,则这个多边形是( )
| A. |
九边形 |
B. |
八边形 |
C. |
七边形 |
D. |
六边形 |
下面是几个一样的小正方体摆出的立体图形的三视图,由三视图可知小正方体的个数为( )

| A. |
6个 |
B. |
5个 |
C. |
4个 |
D. |
3个 |
某学习小组做"用频率估计概率"的试验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的试验最有可能的是( )

| A. |
袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球 |
| B. |
掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数 |
| C. |
先后两次掷一枚质地均匀的硬币,两次都出现反面 |
| D. |
先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9 |
若以二元一次方程 x+2 y﹣ b=0的解为坐标的点( x, y)都在直线 y=﹣ x+ b﹣1上,则常数 b=( )
| A. |
|
B. |
2 |
C. |
﹣1 |
D. |
1 |
随着"三农"问题的解决,某农民近两年的年收入发生了明显变化,已知前年和去年的收入分别是60000元和80000元,下面是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图.依据统计图得出的以下四个结论正确的是( )
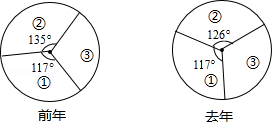
| A. |
①的收入去年和前年相同 |
| B. |
③的收入所占比例前年的比去年的大 |
| C. |
去年②的收入为2.8万 |
| D. |
前年年收入不止①②③三种农作物的收入 |
顺次连接平面上 A、 B、 C、 D四点得到一个四边形,从① AB∥ CD② BC= AD③∠ A=∠ C④∠ B=∠ D四个条件中任取其中两个,可以得出"四边形 ABCD是平行四边形"这一结论的情况共有( )
| A. |
5种 |
B. |
4种 |
C. |
3种 |
D. |
1种 |
下列运算及判断正确的是( )
| A. |
﹣5× ÷(﹣ )×5=1 |
| B. |
方程(x 2+x﹣1) x +3=1有四个整数解 |
| C. |
若a×567 3=10 3,a÷10 3=b,则a×b= |
| D. |
有序数对(m 2+1,|m|)在平面直角坐标系中对应的点一定在第一象限 |
若满足 < x≤1的任意实数 x,都能使不等式2 x 3﹣ x 2﹣ mx>2成立,则实数 m的取值范围是( )
| A. |
m<﹣1 |
B. |
m≥﹣5 |
C. |
m<﹣4 |
D. |
m≤﹣4 |
文具店销售某种笔袋,每个18元,小华去购买这种笔袋,结账时店员说:"如果你再多买一个就可以打九折,价钱比现在便宜36元",小华说:"那就多买一个吧,谢谢,"根据两人的对话可知,小华结账时实际付款 元.
已知函数 y=(2 k﹣1) x+4( k为常数),若从﹣3≤ k≤3中任取 k值,则得到的函数是具有性质" y随 x增加而增加"的一次函数的概率为 .
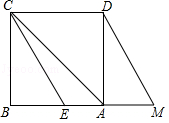
如图,已知正方形 ABCD,点 M是边 BA延长线上的动点(不与点 A重合),且 AM< AB,△ CBE由△ DAM平移得到.若过点 E作 EH⊥ AC, H为垂足,则有以下结论:①点 M位置变化,使得∠ DHC=60°时,2 BE= DM;②无论点 M运动到何处,都有 DM= HM;③无论点 M运动到何处,∠ CHM一定大于135°.其中正确结论的序号为 .
如图,已知 A、 F、 C、 D四点在同一条直线上, AF= CD, AB∥ DE,且 AB= DE.
(1)求证:△ ABC≌△ DEF;
(2)若 EF=3, DE=4,∠ DEF=90°,请直接写出使四边形 EFBC为菱形时 AF的长度.

下表是随机抽取的某公司部分员工的月收入资料.
月收入/元 |
45000 |
18000 |
10000 |
5500 |
5000 |
3400 |
3000 |
2000 |
人数 |
1 |
1 |
1 |
3 |
6 |
1 |
11 |
2 |
(1)请计算以上样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论;
(3)指出谁的推断比较科学合理,能真实地反映公司全体员工月收入水平,并说出另一个人的推断依据不能真实反映公司全体员工月收入水平的原因.
如图,已知 A(6,0), B(8,5),将线段 OA平移至 CB,点 D在 x轴正半轴上(不与点 A重合),连接 OC, AB, CD, BD.
(1)求对角线 AC的长;
(2)设点 D的坐标为( x,0),△ ODC与△ ABD的面积分别记为 S 1, S 2.设 S= S 1﹣ S 2,写出 S关于 x的函数解析式,并探究是否存在点 D使 S与△ DBC的面积相等?如果存在,用坐标形式写出点 D的位置;如果不存在,说明理由.

如图,一座山的一段斜坡 BD的长度为600米,且这段斜坡的坡度 i=1:3(沿斜坡从 B到 D时,其升高的高度与水平前进的距离之比).已知在地面 B处测得山顶 A的仰角为33°,在斜坡 D处测得山顶 A的仰角为45°.求山顶 A到地面 BC的高度 AC是多少米?(结果用含非特殊角的三角函数和根式表示即可)

已知变量 x、 y对应关系如下表已知值呈现的对应规律.
x |
… |
﹣4 |
﹣3 |
﹣2 |
﹣1 |
1 |
2 |
3 |
4 |
… |
y |
… |
|
|
1 |
2 |
﹣2 |
﹣1 |
﹣ |
﹣ |
… |
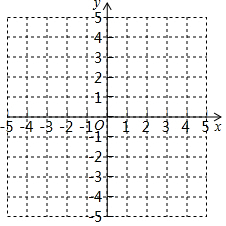
(1)依据表中给出的对应关系写出函数解析式,并在给出的坐标系中画出大致图象;
(2)在这个函数图象上有一点 P( x, y)( x<0),过点 P分别作 x轴和 y轴的垂线,并延长与直线 y= x﹣2交于 A、 B两点,若△ PAB的面积等于 ,求出 P点坐标.
已知关于 x的一元二次方程 ax 2+ bx+ c=0( a≠0)有两个实数根 x 1, x 2,请用配方法探索有实数根的条件,并推导出求根公式,证明 x 1• x 2= .
如图,已知 BC⊥ AC,圆心 O在 AC上,点 M与点 C分别是 AC与⊙ O的交点,点 D是 MB与⊙ O的交点,点 P是 AD延长线与 BC的交点,且 = .
(1)求证: PD是⊙ O的切线;
(2)若 AD=12, AM= MC,求 的值.

某市计划在十二年内通过公租房建设,解决低收入人群的住房问题.已知前7年,每年竣工投入使用的公租房面积 y(单位:百万平方米),与时间 x(第 x年)的关系构成一次函数,(1≤ x≤7且 x为整数),且第一和第三年竣工投入使的公租房面积分别为 和 百万平方米;后5年每年竣工投入使用的公租房面积 y(单位:百万平方米),与时间 x(第 x年)的关系是 y=﹣ x+ (7< x≤12且 x为整数).
(1)已知第6年竣工投入使用的公租房面积可解决20万人的住房问题,如果人均住房面积,最后一年要比第6年提高20%,那么最后一年竣工投入使用的公租房面积可解决多少万人的住房问题?
(2)受物价上涨等因素的影响,已知这12年中,每年竣工投入使用的公租房的租金各不相同,且第一年,一年38元/ m 2,第二年,一年40元/ m 2,第三年,一年42元/ m 2,第四年,一年44元/ m 2……以此类推,分析说明每平方米的年租金和时间能否构成函数,如果能,直接写出函数解析式;
(3)在(2)的条件下,假设每年的公租房当年全部出租完,写出这12年中每年竣工投入使用的公租房的年租金 W关于时间 x的函数解析式,并求出 W的最大值(单位:亿元).如果在 W取得最大值的这一年,老张租用了58 m 2的房子,计算老张这一年应交付的租金.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号