2020年辽宁省抚顺市中考数学试卷
某校九年级进行了3次数学模拟考试,甲、乙、丙、丁4名同学3次数学成绩的平均分都是129分,方差分别是 , , , ,则这4名同学3次数学成绩最稳定的是
| A. |
甲 |
B. |
乙 |
C. |
丙 |
D. |
丁 |
随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递80件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件 件,根据题意可列方程为
| A. |
|
B. |
|
| C. |
|
D. |
|
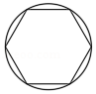
如图,四边形 是菱形,对角线 , 相交于点 , . ,点 是 上一点,连接 ,若 ,则 的长是
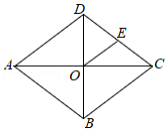
| A. |
2 |
B. |
|
C. |
3 |
D. |
4 |
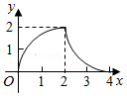
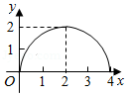
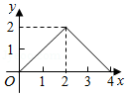
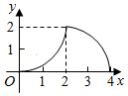
如图,在 中, , , 于点 .点 从点 出发,沿 的路径运动,运动到点 停止,过点 作 于点 ,作 于点 .设点 运动的路程为 ,四边形 的面积为 ,则能反映 与 之间函数关系的图象是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在 中, , 分别是 和 的中点,连接 ,点 是 的中点,连接 并延长,交 的延长线于点 .若 ,则 的长为 .
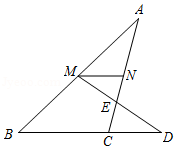
如图,在 中, , ,分别以点 和 为圆心,以大于 的长为半径作弧,两弧相交于点 和 ,作直线 ,交 于点 ,连接 ,若 ,则 的长为 .
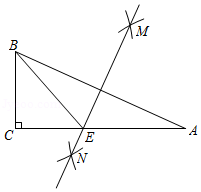
如图,在 中, ,点 在反比例函数 的图象上,点 , 在 轴上, ,延长 交 轴于点 ,连接 ,若 的面积等于1,则 的值为 .

如图,四边形 是矩形,延长 到点 ,使 ,连接 ,点 是 的中点,连接 , ,得到△ ;点 是 的中点,连接 , ,得到△ ;点 是 的中点,连接 , ,得到△ ; ;按照此规律继续进行下去,若矩形 的面积等于2,则△ 的面积为 .(用含正整数 的式子表示)
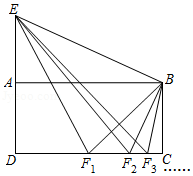
为培养学生的阅读习惯,某中学利用学生课外时间开展了以"走近名著"为主题的读书活动.为了有效了解学生课外阅读情况,现随机调查了部分学生每周课外阅读的时间,设被调查的每名学生每周课外阅读的总时间为 小时,将它分为4个等级: , , , ,并根据调查结果绘制了如图两幅不完整的统计图:
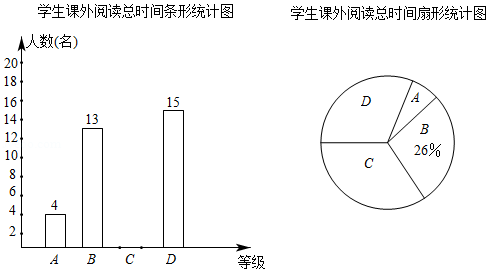
请你根据统计图的信息,解决下列问题:
(1)本次共调查了 名学生;
(2)在扇形统计图中,等级 所对应的扇形的圆心角为 ;
(3)请补全条形统计图;
(4)在等级 中有甲、乙、丙、丁4人表现最为优秀,现从4人中任选2人作为学校本次读书活动的宣传员,用列表或画树状图的方法求恰好选中甲和乙的概率.
某校计划为教师购买甲、乙两种词典.已知购买1本甲种词典和2本乙种词典共需170元,购买2本甲种词典和3本乙种词典共需290元.
(1)求每本甲种词典和每本乙种词典的价格分别为多少元?
(2)学校计划购买甲种词典和乙种词典共30本,总费用不超过1600元,那么最多可购买甲种词典多少本?
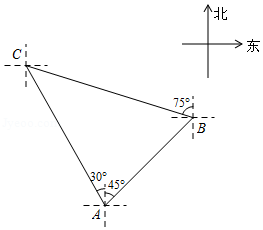
如图,我国某海域有 , 两个港口,相距80海里,港口 在港口 的东北方向,点 处有一艘货船,该货船在港口 的北偏西 方向,在港口 的北偏西 方向,求货船与港口 之间的距离.(结果保留根号)
超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量 (瓶 与每瓶售价 (元 之间满足一次函数关系(其中 ,且 为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.
(1)求 与 之间的函数关系式;
(2)设超市销售该品牌洗手液每天销售利润为 元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
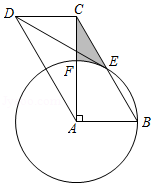
如图,在平行四边形 中, 是对角线, ,以点 为圆心,以 的长为半径作 ,交 边于点 ,交 于点 ,连接 .
(1)求证: 与 相切;
(2)若 , ,求阴影部分的面积.
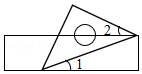
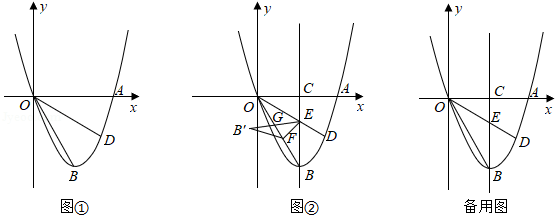
如图,射线 和射线 相交于点 , ,且 .点 是射线 上的动点(点 不与点 和点 重合),作射线 ,并在射线 上取一点 ,使 ,连接 , .
(1)如图①,当点 在线段 上, 时,请直接写出 的度数;
(2)如图②,当点 在线段 上, 时,请写出线段 , , 之间的数量关系,并说明理由;
(3)当 , 时,请直接写出 的值.





 粤公网安备 44130202000953号
粤公网安备 44130202000953号