湖南省益阳市高三四月调研考试文科数学试卷
如图,在△ 中,
中, 分别是
分别是 的中点,若
的中点,若 (
( ),且点
),且点 落在四边形
落在四边形 内(含边界),则
内(含边界),则 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
在某市2015年“创建省文明卫生城市”知识竞赛中 ,考评组从中抽取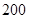 份试卷进行分析,其分数的频率分布直方图如右图所示,则分数在区间
份试卷进行分析,其分数的频率分布直方图如右图所示,则分数在区间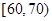 上的人数大约有 人.
上的人数大约有 人.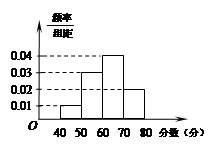
如图所示,矩形长为3,宽为2,在矩形内随机撒200颗黄豆,数得落在椭圆内的黄豆数为160颗,依据此实验数据可以估计出椭圆的面积约为 .
(本小题满分12分)等差数列 满足:
满足: ,
, ,其中
,其中 为数列
为数列 前
前 项和.
项和.
(Ⅰ)求数列 通项公式;
通项公式;
(Ⅱ)若 ,且
,且 ,
, ,
, 成等比数列,求
成等比数列,求 的值.
的值.
(本小题满分12分)某城市持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一,为此该城市实施了机动车尾号限行政策。现有家报社想调查了解该市区公民对“车辆限行”的态度,在该城市里随机抽查了50人,将调查情况进行整理后制成下表:
| 年龄(岁) |
[15,25) |
[25,35) |
[35,45) |
[45,55) |
[55,65) |
[65,75] |
| 频 数 |
2 |
4 |
20 |
14 |
5 |
5 |
| 支持的人数 |
1 |
3 |
15 |
11 |
4 |
4 |
(Ⅰ)请估计该市公民对“车辆限行”的支持率(答案用百分比表示);
(Ⅱ)若从年龄在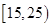 ,
,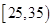 的被调查者中采用分层抽样选取3人进行跟踪调查,求选取的3人中有2人不支持“车辆限行”的概率.
的被调查者中采用分层抽样选取3人进行跟踪调查,求选取的3人中有2人不支持“车辆限行”的概率.
(本小题满分12分)已知在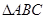 中,三条边
中,三条边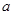 、
、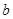 、
、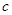 所对的角分别为
所对的角分别为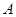 、
、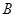 、
、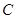 ,向量
,向量 ,
, ,且满足
,且满足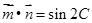 .
.
(Ⅰ)求角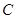 的大小;
的大小;
(Ⅱ)若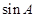 ,
,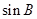 ,
,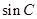 成等比数列,且
成等比数列,且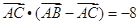 ,求边
,求边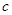 的值并求
的值并求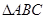 外接圆的面积.
外接圆的面积.
(本小题满分13分)如图,四棱锥 ,侧面
,侧面 是边长为
是边长为 的正三角形,且与底面垂直,底面
的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 四点共面?若存在,指出点
四点共面?若存在,指出点 的位置并证明;若不存在,请说明理由;
的位置并证明;若不存在,请说明理由;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
(本小题满分13分)已知抛物线的顶点在原点,焦点 在
在 轴上,且抛物线上横坐标为1的点到
轴上,且抛物线上横坐标为1的点到 的距离为2 ,过点
的距离为2 ,过点 的直线交抛物线于
的直线交抛物线于 ,
, 两点.
两点.
(Ⅰ)求抛物线的方程;
(Ⅱ)若 ,求直线
,求直线 的斜率;
的斜率;
(Ⅲ)设点 在线段
在线段 上运动,原点
上运动,原点 关于点
关于点 的对称点为
的对称点为 ,求四边形
,求四边形 面积的最小值.
面积的最小值.
 为虚数单位,复数
为虚数单位,复数 对应的点位于
对应的点位于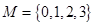 ,
,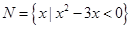 ,则
,则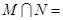
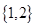
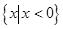
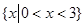
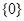
 ,则
,则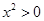 ”的否命题是
”的否命题是 ,则
,则
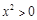 ,则
,则 ,则
,则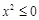 ,则
,则 轴上的椭圆的离心率为
轴上的椭圆的离心率为 ,它的长轴长等于圆
,它的长轴长等于圆 的半径,则椭圆的标准方程是
的半径,则椭圆的标准方程是



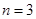 时,执行如图所示的程序框图,输出的
时,执行如图所示的程序框图,输出的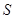 值为
值为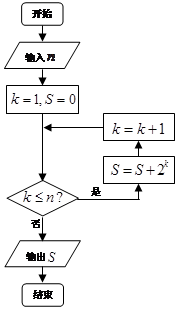
 ,
, ,
, ,则
,则 ,
, ,
, 的大小关系是
的大小关系是








 围成的区域为
围成的区域为 ,能够把区域
,能够把区域



 ,若
,若 恒成立,则
恒成立,则 的取值范围是
的取值范围是



 )与曲线
)与曲线 上的点的最短距离为 .
上的点的最短距离为 .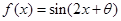 的图象向右平移个单位长度后得到函数
的图象向右平移个单位长度后得到函数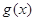 的图象,若
的图象,若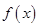 ,
,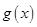 的图象的对称轴重合,则
的图象的对称轴重合,则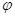 的值为 .
的值为 .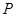
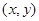 在直线
在直线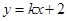 上,记
上,记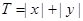 ,若使
,若使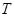 取得最小值的点
取得最小值的点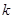 的取值是 .
的取值是 . ,其图象记为曲线
,其图象记为曲线 .
. 在
在 处取得极值为
处取得极值为 ,求
,求 的值;
的值; ,且
,且 ,过点
,过点 作曲线
作曲线 (点
(点 异于点
异于点 ).
). ;
; ,求
,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号