期中备考总动员高三文数学模拟卷【浙江】9
已知a∈R,则“a>2”是“a2>2a”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
一块橡胶泥表示的几何体的三视图如图所示,将该橡胶泥揉成一个底面边长为8的正三角形的三棱锥,则这个三棱锥的高为( )

A.3 |
B.6 |
C.9 |
D.18 |
设A,B,C是圆x2+y2=1上不同的三个点,且 ·
· =0,存在实数λ,μ,使得
=0,存在实数λ,μ,使得 =λ
=λ +μ
+μ ,实数λ,μ的关系为( )
,实数λ,μ的关系为( )
| A.λ2+μ2=1 | B. + + =1 =1 |
| C.λμ=1 | D.λ+μ=1 |
如图,已知椭圆 ,双曲线
,双曲线 ,若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )
,若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )

| A.5 | B. |
C. |
D. |
(原创)已知数列{ }为等差数列,数列{
}为等差数列,数列{ }满足
}满足 =
=

 ,{
,{ }的前n项和为
}的前n项和为 ,若3
,若3 =8
=8 >0,则
>0,则 取得最大值时,n的值为( )
取得最大值时,n的值为( )
| A.13 | B.14 | C.15 | D.16 |
(改编)函数 ,其中
,其中 ,若动直线
,若动直线 与函数
与函数 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为 ,下面关于
,下面关于 最大值的结论正确的是( )
最大值的结论正确的是( )
| A.最大值是1 | B.最大值是3 |
C.最大值是 |
D.没有最大值 |
(原创) ,若
,若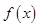 在[
在[ ,
, ]上是增函数,则ω的取值范围是_________;若
]上是增函数,则ω的取值范围是_________;若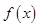 在[
在[ ,
, ]上的最小值为-1,则ω的取值范围是_________.
]上的最小值为-1,则ω的取值范围是_________.
如图放置的边长为1的正方形PABC沿 轴滚动.设顶点P(
轴滚动.设顶点P( ,y)的轨迹方程是
,y)的轨迹方程是 ,则
,则 的最小正周期为 ;
的最小正周期为 ; 在其两个相邻零点间的图像与
在其两个相邻零点间的图像与 轴所围区域的面积为 .
轴所围区域的面积为 .

一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为 ,则该三角形的斜边长为 .
,则该三角形的斜边长为 .
(本小题满分15分)如图所示,正方形 与直角梯形
与直角梯形 所在平面互相垂直,
所在平面互相垂直, ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)求四面体 的体积.
的体积.
(原创)已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在 ,使得
,使得 成立.
成立.
(1)函数 是否属于集合
是否属于集合 ?说明理由;
?说明理由;
(2)设函数 ,求
,求 的取值范围;
的取值范围;
(3)设函数 图象与函数
图象与函数 的图象有交点,证明:函数
的图象有交点,证明:函数 .
.
已知数列{ }中,
}中, ,且
,且 对任意正整数都成立,数列{
对任意正整数都成立,数列{ }的前n项和为
}的前n项和为
(1)若 ,且
,且 ,求a;
,求a;
(2)是否存在实数k,使数列{ }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若 .
.
 为奇函数,且当x>0时,,
为奇函数,且当x>0时,, 则
则 ( )
( ) ,则( )
,则( )



 成等差数列,则公比
成等差数列,则公比 _________;
_________; =_________.
=_________. ,
, 为正实数,且
为正实数,且 ,则
,则 的最大值为 ;
的最大值为 ; 的最大值为 .
的最大值为 . ,直线
,直线 为直线
为直线 上一点,若圆
上一点,若圆 上存在两点
上存在两点 ,使得
,使得 ,则点A的横坐标的取值范围是 .
,则点A的横坐标的取值范围是 . ,
, 满足
满足 ,若目标函数
,若目标函数 的最大值为
的最大值为 ,最小值为
,最小值为 ,则实数
,则实数 的取值范围是 .
的取值范围是 . 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 .
. 的大小;
的大小; ,求△
,求△ 的面积.
的面积. 的两个焦点为
的两个焦点为 、
、 ,短轴两个端点为
,短轴两个端点为  、
、 .已知
.已知 、
、 、
、 成等比数列,
成等比数列, ,与
,与 轴不垂直的直线
轴不垂直的直线 与 C 交于不同的两点
与 C 交于不同的两点 、
、 ,记直线
,记直线 、
、 的斜率分别为
的斜率分别为 、
、 ,且
,且 .
.
 的方程;
的方程; 轴相交于定点,并求出定点坐标;
轴相交于定点,并求出定点坐标; 的中点
的中点 落在四边形
落在四边形 内(包括边界)时,求直线
内(包括边界)时,求直线  粤公网安备 44130202000953号
粤公网安备 44130202000953号