期中备考总动员高三文数学模拟卷【浙江】8
设 ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 则 则 |
B.若 则 则 |
C.若 则 则 |
D.若 则 则 |
来源:2015年期中备考总动员高三文数学模拟卷【浙江】8
若 是实数,则“
是实数,则“ ”是“
”是“ ”或“
”或“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
来源:2015年期中备考总动员高三文数学模拟卷【浙江】8
若 是双曲线
是双曲线 上一点,且满足
上一点,且满足 ,则该点
,则该点 一定位于双曲线( )
一定位于双曲线( )
| A.右支上 | B.上支上 | C.右支上或上支上 | D.不能确定 |
来源:2015年期中备考总动员高三文数学模拟卷【浙江】8
已知 是椭圆
是椭圆 和双曲线
和双曲线 的公共顶
的公共顶
点. 是双曲线上的动点,
是双曲线上的动点, 是椭圆上的动点(
是椭圆上的动点( 、
、 都异于
都异于 、
、 ),且满足
),且满足 ,其中
,其中 ,设直线
,设直线 、
、 、
、 、
、 的斜率 分别记为
的斜率 分别记为 ,
,  ,则
,则
来源:2015年期中备考总动员高三文数学模拟卷【浙江】8
如图,正方体ABCD—A1B1C1D1,

则下列四个命题:
①P在直线BC1上运动时,三棱锥A—D1PC的体积不变;
②P在直线BC1上运动时,直线AP与平面ACD1所成角的大小不变;
③P在直线BC1上运动时,二面角P—AD1—C的大小不变;
④M是平面A1B1C1D1上到点D和C1距离相等的点,则M点的轨迹是过D1点的直线D1A1.
其中真命题的编号是 .
来源:2015年期中备考总动员高三文数学模拟卷【浙江】8
若 是各项均不为零的等差数列,公差为
是各项均不为零的等差数列,公差为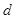 ,
, 为其前
为其前 项和,且满足
项和,且满足 ,
, .数列
.数列 满足
满足 ,
, 为数列
为数列 的前
的前 项和.
项和.
(Ⅰ)求 和
和 ;
;
(Ⅱ)是否存在正整数 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
来源:2015年期中备考总动员高三文数学模拟卷【浙江】8
如图, 在直三棱柱 中,
中, ,
, ,
, .
.
(1)求证: ;
;
(2)问:是否在 线段上存在一点
线段上存在一点 ,使得
,使得 平面
平面 ?若存在,请证明;若不存在,请说明理由.
?若存在,请证明;若不存在,请说明理由.
来源:2015年期中备考总动员高三文数学模拟卷【浙江】8
(原创)已知
(1)若a>b>c>1,且a、b、c成等差数列,求证: ;
;
(2)若m>n>0时,有 ,求证:
,求证: .
.
来源:2015年期中备考总动员高三文数学模拟卷【浙江】8




 中,
中, ,
, ,
, ,
, 为
为 边上的高,
边上的高, 为
为 ,则
,则 的值为
的值为



 中
中 =10,
=10, 的最大值( )
的最大值( )
 有
有 个零点,则实数
个零点,则实数 的取值范围是( )
的取值范围是( )



 满足
满足 ,则
,则 的取值范围是 ( )
的取值范围是 ( ) ]
]


 则
则 ;
; .
. 时,
时, ,则
,则 中,最大的是 ;最小的是 .
中,最大的是 ;最小的是 . 在圆
在圆 上,则函数
上,则函数 的最小正周期是 ;最小值是 .
的最小正周期是 ;最小值是 . ,则
,则 ,
, 的最小值为 .
的最小值为 . )如下图所示,此几何体的体积是_____________
)如下图所示,此几何体的体积是_____________

 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
. 的值;
的值; 的值.
的值. ,
, 分别是椭圆
分别是椭圆
 的左、右焦点,过
的左、右焦点,过 与
与 轴垂直的直线交椭圆于点
轴垂直的直线交椭圆于点 ,且
,且

 ,问是否存在直线
,问是否存在直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,
, ,且
,且 的垂直平分线恰好过
的垂直平分线恰好过 点?若存在,求出直线
点?若存在,求出直线 粤公网安备 44130202000953号
粤公网安备 44130202000953号