期中备考总动员高三理数学模拟卷【山东】4
已知对称中心为坐标原点的椭圆与双曲线有共同的焦点, 其左、右焦点都在 轴上,分别设为
轴上,分别设为 ,
, ,它们在第一象限的交点为
,它们在第一象限的交点为 ,
, 是以
是以 为底边的等腰三角形.若
为底边的等腰三角形.若 ,且椭圆的离心率为
,且椭圆的离心率为 ,则双曲线的离心率为 .
,则双曲线的离心率为 .
来源:2015年期中备考总动员高三理数学模拟卷【山东】4
(本小题满分12分)某大学准备在开学时举行一次大学一年级学生座谈会,拟邀请 名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
| 学院 |
机械工程学院 |
海洋学院 |
医学院 |
经济学院 |
| 人数 |
 |
 |
 |
 |
(Ⅰ)从这 名学生中随机选出
名学生中随机选出 名学生发言,求这
名学生发言,求这 名学生中任意两个均不属于同一学院的概率;
名学生中任意两个均不属于同一学院的概率;
(Ⅱ)从这 名学生中随机选出
名学生中随机选出 名学生发言,设来自医学院的学生数为
名学生发言,设来自医学院的学生数为 ,求随机变量
,求随机变量 的概率分布列和数学期望.
的概率分布列和数学期望.
来源:2015年期中备考总动员高三理数学模拟卷【山东】4
(本小题满分12分)如图,在四棱柱 中,侧棱
中,侧棱 底面
底面  ,底面
,底面 是直角梯形,
是直角梯形, ,
, ,
,  ,
, ,
, 为
为 中点.
中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)若 ,求平面
,求平面 和平面
和平面 所成角(锐角)的余弦值.
所成角(锐角)的余弦值.
来源:2015年期中备考总动员高三理数学模拟卷【山东】4
(本小题满分12分)已知数列 是等差数列,
是等差数列, 为
为 的前
的前 项和,且
项和,且 ,
, ;数列
;数列 对任意
对任意 ,总有
,总有 成立.
成立.
(Ⅰ)求数列 和
和 的通项公式;
的通项公式;
(Ⅱ)记 ,求数列
,求数列 的前
的前 项和
项和 .
.
来源:2015年期中备考总动员高三理数学模拟卷【山东】4
(本小题满分13分)已知椭圆 与直线
与直线 相交于
相交于 、
、 两不同点,且直线
两不同点,且直线 与圆
与圆 相切于点
相切于点 (
( 为坐标原点).
为坐标原点).
(Ⅰ)证明: ;
;
(Ⅱ)设 ,求实数
,求实数 的取值范围.
的取值范围.
来源:2015年期中备考总动员高三理数学模拟卷【山东】4
 ,
, ,则
,则 ( )
( )



 ,则
,则 ( )
( )



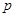 :
: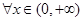 ,
,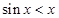 ,则
,则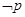 为( )
为( ) ,使得
,使得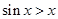
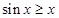
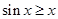
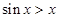
 和
和 垂直,则
垂直,则 的最小值为( )
的最小值为( )



 中,若
中,若 ,则
,则 ( )
( ) ,则函数
,则函数 的零点个数为( )
的零点个数为( )




 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( )



 的图像为( )
的图像为( )
 在圆
在圆 上,抛物线上
上,抛物线上 任意一点
任意一点 到直线
到直线 的距离为
的距离为 ,则
,则 的最小值等于( )
的最小值等于( )
 与曲线
与曲线 相切于点
相切于点 ,则
,则 的值为 .
的值为 . 的展开式中的常数项为
的展开式中的常数项为 ,则
,则 .
.
 ,则
,则 的最小值为 .
的最小值为 . 的内角
的内角 所对的边分别为
所对的边分别为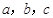 ,已知
,已知 ,
, .
.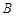 ;
; 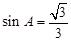 ,求
,求 ,
, ,
, .
. 的图象在原点处的切线
的图象在原点处的切线 与函数
与函数 的图象相切,求实数
的图象相切,求实数 的值;
的值; 在
在 上单调递减,求实数
上单调递减,求实数 ,总存在
,总存在 ,且
,且 满
满
 ,其中
,其中 为自然对数的底数,求实数
为自然对数的底数,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号