期中备考总动员高三理数学模拟卷【广东】7
已知全集U={-2,-1,0,1,2,3,4,5,6},集合M={大于 且小于4的整数},则
且小于4的整数},则 ( )
( )
A. |
B.{-2,-1,5,6} |
| C.{0,1,2,3,4} | D.{-2,-1,4,5,6} |
过抛物线: 的焦点F作倾斜角为
的焦点F作倾斜角为 的直线
的直线 ,若直线
,若直线 与抛物线在第一象限的交点为A,并且点A也在双曲线:
与抛物线在第一象限的交点为A,并且点A也在双曲线: 的一条渐近线上,则双曲线的离心率为 ;
的一条渐近线上,则双曲线的离心率为 ;
(几何证明选讲)如图所示,AB是⊙O的直径,过圆上一点E作切线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.若CB=2, CE=4,则AD的长为 .

【改编】(本小题满分12分)已知向量
 ,函数
,函数 .
.
(1)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(2)在 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,求
,求 的面积.
的面积.
(本小题满分12分)近年来空气污染是一个生活中重要的话题, PM2.5就是其中一个指标。PM2.5指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值在35微克/立方米以下空气质量为一级:在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.淮北相山区2014年12月1日至I0日每天的PM2.5监测数据如茎叶图所示.
(1)期间的某天小刘来此地旅游,求当天PM2.5日均监测数据未超标的概率;
(2)陶先生在此期间也有两天经过此地,这两天此地PM2.5监测数据均未超标.请计算出这两天空气质量恰好有一天为一级的概率;
(3)从所给10天的数据中任意抽取三天数据,记 表示抽到PM2.5监测数据超标的天数,求
表示抽到PM2.5监测数据超标的天数,求 的分布列及期望.
的分布列及期望.
(本小题满分14分)已知 为等比数列,其中
为等比数列,其中 ,且
,且 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分14分)已知在四棱锥 中,底面
中,底面 是矩形,且
是矩形,且 ,
, ,
, 平面
平面 ,
, ,
, 分别是线段
分别是线段 ,
, 的中点.
的中点.
(1)判断并说明 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不
的值;若不
存在,请说明理由;
(2)若 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值.
在平面直角坐标系 中,点A、B的坐标分别是
中,点A、B的坐标分别是 、
、 ,直线AM、BM相交于点M,且它们的斜率之积是
,直线AM、BM相交于点M,且它们的斜率之积是 .
.
(1)求点M的轨迹 方程;
方程;
(2)若直线 经过点
经过点 ,与轨迹
,与轨迹 有且仅有一个公共点,求直线
有且仅有一个公共点,求直线 的方程.
的方程.

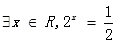
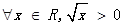
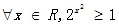
 为虚数单位,且
为虚数单位,且 ,则
,则 的值为 ( )
的值为 ( )

 ,则
,则 =( )
=( )


 ,若向量
,若向量 与向量
与向量 的夹角为
的夹角为 ,则
,则 ( )
( )




 对任意
对任意 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 =( )
=( )







 在点(0,2)处的切线与直线
在点(0,2)处的切线与直线 平行,则
平行,则 =_____.
=_____. 的展开式中各项系数的和为
的展开式中各项系数的和为  满足:
满足: ,则
,则 的取值范围是 ,
的取值范围是 , 与函数
与函数 ,
, ,则两个函数在
,则两个函数在
 上交点个数为 ;
上交点个数为 ; 与直线
与直线 平行,则常数
平行,则常数 的值为_______.
的值为_______. (
( 是常数).
是常数). ,
, 、
、 是函数
是函数 的极值点,试证明曲线
的极值点,试证明曲线 对称;
对称; ,使得
,使得 ,
, 恒成立?若存在,求常数
恒成立?若存在,求常数 ,若点
,若点 的对称点为
的对称点为 ,则
,则 粤公网安备 44130202000953号
粤公网安备 44130202000953号