高考原创文科数学预测卷 02(山东卷)
某校高一、高二、高三分别有学生1600名、1200名、800名,为了解该校高中学生的牙齿健康状况,按各年级的学生数进行分层抽样,若高三抽取20名学生,则高一、高二共抽取的学生数为( )
| A.70 | B.60 | C.55 | D.40 |
同时具有性质“⑴ 最小正周期是 ;⑵ 图象关于直线
;⑵ 图象关于直线 对称;⑶ 在
对称;⑶ 在 上是减函数”的一个函数可以是( )
上是减函数”的一个函数可以是( )
A. |
B. |
C. |
D. |
设 是一个各位数字都不是0且没有重复数字的三位数.将组成
是一个各位数字都不是0且没有重复数字的三位数.将组成 的3个数字按从小到大排成的三位数记为
的3个数字按从小到大排成的三位数记为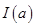 ,按从大到小排成的三位数记为
,按从大到小排成的三位数记为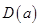 (例如
(例如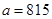 ,则
,则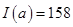 ,
,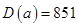 ).阅读如图所示的程序框图,运行相应的程序,任意输入一个
).阅读如图所示的程序框图,运行相应的程序,任意输入一个 ,输出的结果
,输出的结果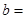 .
.

定义:分子为1且分母为正整数的分数叫做单位分数.我们可以把1拆分为无穷多个不同的单位分数之和.例如: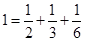 ,
,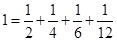 ,
,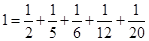 , 依此方法可得:
, 依此方法可得: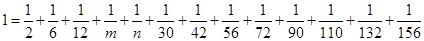 ,其中
,其中 ,则
,则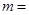 ;
;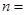 .
.
对定义在区间D上的函数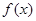 和
和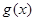 ,如果对任意
,如果对任意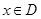 ,都有
,都有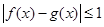 成立,那么称函数
成立,那么称函数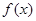 在区间D上可被
在区间D上可被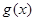 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
①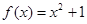 在区间
在区间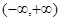 上可被
上可被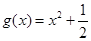 替代;
替代;
②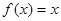 可被
可被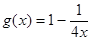 替代的一个“替代区间”为
替代的一个“替代区间”为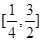 ;
;
③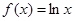 在区间
在区间 可被
可被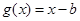 替代,则
替代,则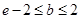 ;
;
④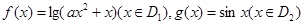 ,则存在实数
,则存在实数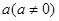 ,使得
,使得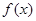 在区间
在区间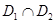 上被
上被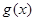 替代;其中真命题的有 .
替代;其中真命题的有 .
(本小题满分12分)泉城济南为增强市民的节水意识,面向全市征召宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(Ⅰ)若从第 组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第
组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(Ⅱ)在(Ⅰ)的条件下,决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
(本小题满分12分)如图所示,已知在四棱锥 中,
中,  ∥
∥ ,
, ,
, ,且
,且

(1)求证: 平面
平面 ;
;
(2)试在线段 上找一点
上找一点 ,使
,使 ∥平面
∥平面 , 并说明理由;
, 并说明理由;
(3)若点 是由(2)中确定的,且
是由(2)中确定的,且 ,求四面体
,求四面体 的体积.
的体积.
(本小题满分12分)已知数列 是等比数列,首项
是等比数列,首项 ,公比
,公比 ,其前
,其前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,
, 为数列
为数列 的前
的前 项和,若
项和,若 恒成立,求
恒成立,求 的最大值.
的最大值.
(本小题满分13分)设函数 ,
, ,函数
,函数 的图象与
的图象与 轴的交点在函数
轴的交点在函数 的图象上,且在此点处两曲线有相同的切线.
的图象上,且在此点处两曲线有相同的切线.
(Ⅰ) 求 、
、 的值;
的值;
(Ⅱ) 设定义在 上的函数
上的函数 的最大值为
的最大值为 ,最小值为
,最小值为 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
 的点位于( )
的点位于( ) ,
,
 ,则
,则 =( )
=( )



 上的奇函数
上的奇函数 满足
满足 ,若
,若 ,
, ,则实数
,则实数 的取值范围为( )
的取值范围为( )



 对任意
对任意 ,总有
,总有 ;
; 是
是 的充分不必要条件则下列命题为真命题的是( )
的充分不必要条件则下列命题为真命题的是( )








 满足约束条件
满足约束条件 ,若
,若 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数 的值为( )
的值为( )


 其中正整数
其中正整数 、
、 (
( )可以任意选取,则
)可以任意选取,则



 与双曲线
与双曲线 (
( )两条渐近线分别交于点
)两条渐近线分别交于点 ,若点
,若点 满足
满足 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )



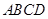 的边长为2,
的边长为2,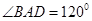 ,点
,点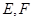 分别在边
分别在边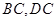 上,
上,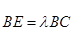 ,
,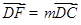 .若
.若 ,
,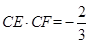 ,则
,则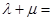 .
.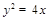 的焦点
的焦点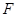 的直线
的直线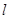 ,与圆
,与圆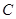 :
: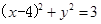 相交于A,B两点,且
相交于A,B两点,且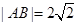 ,则
,则 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量 ,
, ,且
,且 .
. 的大小;
的大小;  ,求
,求

 的右焦点为
的右焦点为 ,且点
,且点 在椭圆
在椭圆 上,
上, 为坐标原点.
为坐标原点. 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 、
、 ,且
,且 为锐角,求直线
为锐角,求直线 的取值范围;
的取值范围;
 上异于其顶点的任一点
上异于其顶点的任一点 ,作圆
,作圆
 的两条切线,切点分别为
的两条切线,切点分别为 (
( 在
在 轴、
轴、 轴上的截距分别为
轴上的截距分别为 、
、 ,证明:
,证明: 为定值.
为定值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号