期中备考总动员高三理数学模拟卷【新课标1】3
如图,在正方形 内任取一点,取到函数
内任取一点,取到函数 的图象与
的图象与 轴正半轴之间(阴影部分)的点的概率等于( )
轴正半轴之间(阴影部分)的点的概率等于( )

A. |
B. |
C. |
D. |
命题P: ;命题q:
;命题q: ,函数
,函数 的图象过点
的图象过点 ,则( )
,则( )
| A.P假q假 | B.P真q假 | C.P假q真 | D.P真q真 |
已知a>0,x,y满足约束条件 ,若z=2x+y的最小值为1,a=( )
,若z=2x+y的最小值为1,a=( )
A. |
B. |
C.1 | D.2 |
函数 的图象向左平移
的图象向左平移 个单位后关于原点对称,则函数f(x)在
个单位后关于原点对称,则函数f(x)在 上的最小值为( )
上的最小值为( )
A. |
B. |
C. |
D. |
已知 为原点,双曲线
为原点,双曲线 (
( )上有一点
)上有一点 ,过
,过 作两条渐近线的平行线,且与两渐近线的交点分别为
作两条渐近线的平行线,且与两渐近线的交点分别为 ,
, ,平行四边形
,平行四边形 的面积为
的面积为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. |
B. |
C. |
D. |
【原创题】已知函数 (
( 为常数)的图像与
为常数)的图像与 轴交于点
轴交于点 ,曲线
,曲线 在点
在点 处的切线斜率为
处的切线斜率为 ,当
,当 时则( )
时则( )
A. |
B. |
C. |
D.无法确定 |
下列说法:
①“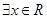 ,使
,使 ”的否定是“
”的否定是“ 使
使 ”;
”;
②函数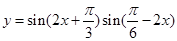 的最小正周期是
的最小正周期是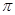 ;
;
③命题“函数f(x)在x=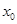 处有极值,则
处有极值,则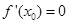 ”的否命题是真命题;
”的否命题是真命题;
④f(x)是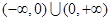 上的奇函数,x>0时的解析式是
上的奇函数,x>0时的解析式是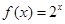 ,则x<0时的解析式为
,则x<0时的解析式为 .
.
其中正确的说法是 .
【原创题】已知函数 的部分图像如图所示,若
的部分图像如图所示,若 ,且
,且 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若将 的图像向左平移
的图像向左平移 个单位长度,得到函数
个单位长度,得到函数 的图像,求函数
的图像,求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
现有4个人去参加娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏。
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(Ⅲ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望 .
.
如图,四棱锥 中,底面ABCD为菱形,
中,底面ABCD为菱形, ,Q是AD的中点.
,Q是AD的中点.
(Ⅰ)若 ,求证:平面PQB
,求证:平面PQB 平面PAD;
平面PAD;
(Ⅱ)若平面APD 平面ABCD,且
平面ABCD,且 ,点M在线段PC上,试确定点M的位置,使二面角
,点M在线段PC上,试确定点M的位置,使二面角 的大小为
的大小为 ,并求出
,并求出 的值.
的值.
.已知椭圆C的中心在原点,焦点在x轴上,离心率等于 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.

(Ⅰ)求椭圆C的方程;
(Ⅱ)点P(2,3), Q(2,-3)在椭圆上,A,B是椭圆上位于直线PQ两恻的动点,
①若直线AB的斜率为 ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足于∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
选修4-1:几何证明选讲
如图, 是
是 ABC的外接圆,D是
ABC的外接圆,D是 的中点,BD 交AC于E
的中点,BD 交AC于E
(1)求证: :
:
(2)若 ,O到AC的距离为1,求
,O到AC的距离为1,求 的半径
的半径
选修4—4:坐标系与参数方程
已知直线l: (t为参数)恒经过椭圆C:
(t为参数)恒经过椭圆C: (为参数)的右焦点F.
(为参数)的右焦点F.
(Ⅰ)求m的值;
(Ⅱ)设直线l与椭圆C交于A,B两点,求|FA|·|FB|的最大值与最小值.
 ,
, ,则
,则 ( )
( )



 .其中i为虚数单位,则a+b=( )
.其中i为虚数单位,则a+b=( ) ,
, 是第三象限的角,则
是第三象限的角,则 =( )
=( )







 ,函数
,函数 是偶函数,若当
是偶函数,若当 时,
时, 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )



 的前n项和
的前n项和 ,且
,且 则过点
则过点 和
和 的直线的一个方向向量是( )
的直线的一个方向向量是( )



 ,
, ,若
,若 ,则
,则 .
. ,满足
,满足 ,则
,则 的取值范围为 .
的取值范围为 . ,则平面BCD被球所截面图形的面积为 .
,则平面BCD被球所截面图形的面积为 . ,
,
 时,若
时,若 在
在 上为减函数,
上为减函数, 在
在 上是增函数,求
上是增函数,求 值;
值; 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 的解集;
的解集; 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号