北京市东城区九年级上学期期末考试数学试卷
以下事件为必然事件的是( )
| A.掷一枚质地均匀的骰子,向上一面的点数是0 |
B.多边形的内角和是 |
| C.二次函数的图象必过原点 |
D.半径为2的圆的周长是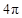 |
将二次函数 的图象向左平移1个单位,再向下平移2个单位后,所得图象的函数表达式是( )
的图象向左平移1个单位,再向下平移2个单位后,所得图象的函数表达式是( )
A. |
B. |
C. |
D. |
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
| A.120° | B.140° | C.150° | D.160° |
如图,在平行四边形ABCD中,点E是边AD的中点,连接EC交对角线BD于点F,则 等于 ( )
等于 ( )
| A.1:2 | B.1:4 | C.1:9 | D.4:9 |
已知二次函数 (a,b,c是常数,且
(a,b,c是常数,且 )的图象如图所示,则一次函数
)的图象如图所示,则一次函数 与反比例函数
与反比例函数 在同一坐标系内的图象大致是( )
在同一坐标系内的图象大致是( )
A. |
B. |
C. |
D. |
如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为( )
A. |
B. |
C. |
D. |
如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ,0),B(0,4),则点B4的坐标为 ,点B2014的坐标为 .
,0),B(0,4),则点B4的坐标为 ,点B2014的坐标为 .
如图,正方形网格中的每个小正方形的边长都是1,顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
已知二次函数 .
.
(1)将 化成
化成 的形式;
的形式;
(2)当 时,
时, 的最小值是 ,最大值是 ;
的最小值是 ,最大值是 ;
(3)当 时,写出
时,写出 的取值范围.
的取值范围.
如图,AB是半圆O的直径,点P(不与点A,B重合)为半圆上一点.将图形沿BP折叠,分别得到点A,O的对称点 ,
, .设∠ABP =α.
.设∠ABP =α.
(1)当α=10°时, °;
°;
(2)当点 落在
落在 上时,求出
上时,求出 的度数.
的度数.
如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.求线段EC的长度.
为了提高学生书写汉字的能力,某市举办了“汉字听写大赛”.为了决定谁将获得仅有的一张观赛券,小王和小李设计了如下的一个规则:不透明的甲袋中有编号分别为1,2,3的乒乓球三个,不透明的乙袋中有编号分别为4,5的乒乓球两个,五个球除了编号不同外,其他均相同.小王和小李分别从甲、乙两个袋子中随机地各摸出一个球,若所摸出的两个球上的数字之和为奇数,则小王去;若两个球上的数字之和为偶数,则小李去.试用列表法或画树状图的方法分析这个规则对双方是否公平?
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如下图,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A处测得高华峰顶F点的俯角为30°,保持方向不变又前进1200米到达点B处测得F点的俯角为45°.请据此计算高华峰的海拔高度.(结果保留整数,参考数值: ≈1.732)
≈1.732)
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与边AC交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)证明:DE是⊙O的切线;
(2)若⊙O的半径R=5,tanA= ,求线段CD的长.
,求线段CD的长.
(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,EF分别是 BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF= ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
已知二次函数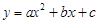 (
( 为常数,且
为常数,且 )的图象过点A(0,1),B(1,-2)和点C(-1,6).
)的图象过点A(0,1),B(1,-2)和点C(-1,6).
(1)求二次函数表达式;
(2)若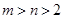 ,比较
,比较 与
与 的大小;
的大小;
(3)将抛物线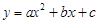 平移,平移后图象的顶点为
平移,平移后图象的顶点为 ,若平移后的抛物线与直线
,若平移后的抛物线与直线 有且只有一个公共点,请用含
有且只有一个公共点,请用含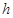 的代数式表示
的代数式表示 .
.
在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1,旋转角为θ(0°<θ<90°),连接AC1、BD1,AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1.
②请直接写出AC1与BD1的位置关系.
(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1.判断AC1与BD1的位置关系,说明理由,并求出k的值.
(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1,设AC1=kBD1.请直接写出k的值和 的值.
的值.
 ,则锐角A的度数是( )
,则锐角A的度数是( )







 (k是常数,且
(k是常数,且 )的图象在第二、四象限,请写出一个符合条件的反比例函数表达式 .
)的图象在第二、四象限,请写出一个符合条件的反比例函数表达式 . ,
, 交AC于点D,若∠
交AC于点D,若∠ =90°,则∠A= 度.
=90°,则∠A= 度.
 在第一象限的图象上有两点
在第一象限的图象上有两点 ,
, ,它们的横坐标分别是2,6,则△
,它们的横坐标分别是2,6,则△ 的面积是 .
的面积是 .
 .
. ,CE=1.求
,CE=1.求 的长度.
的长度.
 与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C(0,-3),其顶点为D,对称轴为直线
与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C(0,-3),其顶点为D,对称轴为直线 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号