暖春三月,贴心开学测 初三数学第六套
下列关于x的方程中,一定是一元二次方程的为( )
| A.ax2+bx+c=0 | B.x2﹣2=(x+3)2 | C. |
D.x2﹣1=0 |
下列事件中,是不可能事件的是( )
| A.买一张电影票,座位号是奇数 |
| B.射击运动员射击一次,命中9环 |
| C.明天会下雨 |
| D.度量三角形的内角和,结果是360° |
下列运算正确的是( )
| A.a6÷a2=a3 | B.3a2b﹣a2b=2 |
| C.(﹣2a3)2=4a6 | D.(a+b)2=a2+b2 |
如图,已知AD∥BC,AC与BD相交于点O,点G是BD的中点,过G作GE∥BC交AC于点E,如果AD=1,BC=3,GE:BC等于( )

| A.1:2 | B.1:3 | C.1:4 | D.2:3 |
如图,山顶一铁塔AB在阳光下的投影CD的长为6米,此时太阳光与地面的夹角∠ACD=60°,则铁塔AB的高为( )

| A.3米 | B.6 米 米 |
C.3 米 米 |
D.2 米 米 |
下列事件是必然事件的是( )
| A.随意掷两个均匀的骰子,朝上面的点数之和为6 |
| B.抛一枚硬币,正面朝上 |
| C.3个人分成两组,一定有2个人分在一组 |
| D.打开电视,正在播放动画片 |
王洪存银行5000元,定期一年后取出3000元,剩下的钱继续定期一年存入,如果每年的年利率不变,到期后取出2750元,则年利率为( )
| A.5% | B.20% | C.15% | D.10% |
如图在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,E是垂足,交AB于D,连接CD,若BD=2,则AC的长是( )

| A.8 | B.4 | C.8 |
D.4 |
已知抛物线y=ax2+bx+c(a<0)过A(﹣3,0)、O(1,0)、B(﹣5,y1)、C(5,y2)四点,则y1与y2的大小关系是( )
| A.y1>y2 | B.y1=y2 | C.y1<y2 | D.不能确定 |
在中国地图册上,联结上海、香港、台湾三地构成一个三角形,用刻度尺测得它们之间的距离如图所示.飞机从台湾直飞上海的距离约为l290千米,那么飞机从台湾绕道香港再到上海的空中飞行距离是 千米.

如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若AB=12,BO=13,AC=4,则OH的值为 .

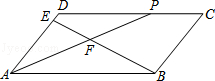
如图,在平行四边形ABCD中,AD=5cm,AP=8cm,AP平分∠DAB,交DC于点P,过点B作BE⊥AD于点E,BE交AP于点F,则tan∠BFP= .
已知O是平面直角坐标系的原点,点A(1,n),B(﹣1,﹣n)(n>0),AB的长是 ,若点C在x轴上,且OC=AC,求点C的坐标.
,若点C在x轴上,且OC=AC,求点C的坐标.
如图(1),格点△ABC(顶点在小正方形的顶点处的三角形称为格点三角形),请在图(2)、(3)、(4)中的6×6的网格中各画一个互不全等的格点三角形,使它们都和△ABC相似.
要求:①其中有一个相似比为 ;②其中有一个面积为5.
;②其中有一个面积为5.
如图在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求点M的坐标;
(2)若反比例函数 y= (x>0)的图象经过点M,通过计算判断点N是否在该函数的图象上;
(x>0)的图象经过点M,通过计算判断点N是否在该函数的图象上;
(3)在(2)的条件下观察图形,当x取何值时,一次函数值小于反比例函数值.
如图,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动,且总保持PQ=PO,过点Q作⊙O的切线交BA的延长线于点C.

(1)当∠QPA=60°时,请你对△QCP的形状做出猜想,并给予证明;
(2)当QP⊥AB时,△QCP的形状是 三角形;
(3)由(1)、(2)得出的结论,请进一步猜想当点P在线段AM上运动到任何位置时,△QCP一定是 三角形.
四边形ABCD是平行四边形,E是对角线AC上一点,射线DE分别交射线CB、AB于点F、G.
(1)如图,如果点F在CB边上,点G在AB边的延长线上,求证: ;
;
(2)如果点F在CB边的延长线上,点G在AB边上,试写出 与
与 之间的一种等量关系,并给出证明.
之间的一种等量关系,并给出证明.
在平面直角坐标系xOy(如图)中,已知A(﹣1,3),B(2,n)两点在二次函数y=﹣ x2+bx+4的图象上.
x2+bx+4的图象上.
(1)求b与n的值;
(2)联结OA、OB、AB,求△AOB的面积;
(3)若点P(不与点A重合)在题目中给出的二次函数的图象上,且∠POB=45°,求点P的坐标.
已知:⊙O的半径长为5,点A、B、C在⊙O上,AB=BC=6,点E在射线BC上.
(1)如图1,联结AE、CE,求证:AE=CE;
(2)如图2,以点C为圆心,CO为半径画弧交半径OB于D,求BD的长.
(3)当OE= 时,求线段AE的长.
时,求线段AE的长.
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,过点C作CM∥BP交PA的延长线于点M.
(1)求证:△ACM≌△BCP;
(2)若PA=1,PB=2,求△PCM的面积.
 =﹣
=﹣
 =﹣0.6
=﹣0.6 =﹣13
=﹣13 =±6
=±6

 =
= ,∠A=30°,求∠B的度数.
,∠A=30°,求∠B的度数.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号