浙江省杭州市余杭区初中联盟学校九年级上学期期中考试数学试卷
在Rt△ABC中,∠A=90°,AB=3,AC=4.若以点C为圆心,画一个半径为4的圆,则点B与⊙C的位置关系为( )
| A.点B在⊙C内 |
| B.点B在⊙C外 |
| C.点B在⊙C上 |
| D.无法判断 |
2014年“十·一”期间,小明与小亮两家准备从农夫乐园、双溪漂流、 超山赏梅选择一景点游玩,小明与小亮通过抽签方式确定景点,则两家抽到同一景点的概率是( )
A. |
B. |
C. |
D. |
下列三个命题:
①圆既是轴对称图形,又是中心对称图形;
②垂直于弦的直径平分这条弦;
③相等圆心角所对的弧相等;
其中是真命题有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
如果将抛物线 向右平移1个单位,那么所得新抛物线的表达式是( )
向右平移1个单位,那么所得新抛物线的表达式是( )
A. |
B. |
C. |
D. |
如图,要拧开一个边长为a=6cm的正六边形螺帽,扳手张开的开口b至少为( )
A. |
B.12mm | C. |
D. |
在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别.摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则估计盒子中大约有白球( )
| A.12个 | B.16个 | C.20个 | D.30个 |
如图是二次函数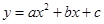 图像的一部分,其对称轴是
图像的一部分,其对称轴是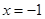 ,且过点(-3,0),下列说法:①
,且过点(-3,0),下列说法:①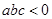 ②
②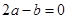 ③
③ ④若
④若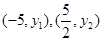 是抛物线上两点,则
是抛物线上两点,则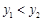 ,其中说法正确的是( )
,其中说法正确的是( )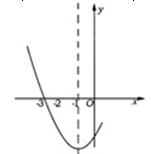
| A.①② | B.②③ | C.①②④ | D.②③④ |
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.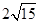 B.8 C.
B.8 C.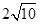 D.
D.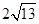
如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为( )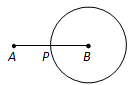

如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为( )
A.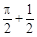 |
B.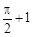 |
C.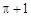 |
D.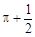 |
如图所示,有一圆形展厅,在其圆形边缘上的点A处安装了一台监视器,它们监控角度是65°.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器 台.
从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数 的系数k,b,则一次函数
的系数k,b,则一次函数 的图象不经过第四象限的概率是 .
的图象不经过第四象限的概率是 .
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于________________
一段抛物线: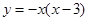
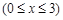 ,记为y 1,它与x轴交于点O,A1;将y 1绕点A1旋转
,记为y 1,它与x轴交于点O,A1;将y 1绕点A1旋转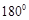 得y 2,交x轴于点A2;将y 2绕点A2旋转
得y 2,交x轴于点A2;将y 2绕点A2旋转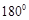 得y 3,,交x轴于点A3;如此进行下去,若P(37,m)在抛物线
得y 3,,交x轴于点A3;如此进行下去,若P(37,m)在抛物线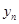 上,则m=____________
上,则m=____________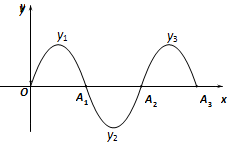
如图,在破残的圆形残片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D,已知AB=8cm,CD=2cm.(本小题满分8分)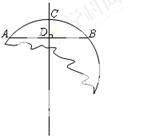
(1)求作此残片所在的圆(尺规作图,不写作法,保留作图痕迹);
(2)求出(1)中所作圆的半径.
(本小题满分8分)
“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要求参赛学生每人交一件作品.现将参赛的50件作品的成绩(单位:分)进行统计如下: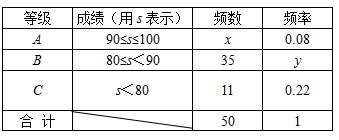
请根据上表提供的信息,解答下列问题:
(1)表中的x的值为 ,y的值为 ;
(2)将本次参赛作品获得A等级的学生一次用A1,A2,A3,…表示,现该校决定从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.
(本小题满分8分)如图,已知AB是⊙O的直径,CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠AEC的度数.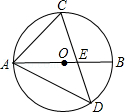
(本小题满分10分)在关于x,y的二元一次方程组 中.
中.
(1)若 ,求方程组的解;
,求方程组的解;
(2)若 ,当
,当 为何值时,S有最小值.
为何值时,S有最小值.
(本小题满分10分)如图:已知⊙O的直径CD为2, 的度数为60°,点B是
的度数为60°,点B是 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的最小值为多少?
的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的最小值为多少?
如图1,在平面直角坐标系中,O为坐标原点,P是反比例函数 图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.(本小题满分10分)
图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.(本小题满分10分)
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;
(3)如图2,Q是反比例函数 图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D,求证:DO·OC=BO·OA.
图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D,求证:DO·OC=BO·OA.
 与x轴仅有一个公共点,则实数k的值为 .
与x轴仅有一个公共点,则实数k的值为 . cm,则∠A的度数为 .
cm,则∠A的度数为 .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号