在一次数学活动课上,某数学老师将 共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字,每一个数字只写在一张卡片上,而且把写有数字的那一面朝下).他先像洗扑克牌一样打乱这些卡片的顺序,然后把甲,乙,丙,丁,戊五位同学叫到讲台上,随机地发给每位同学两张卡片,并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上,写出的结果依次是:甲:11;乙:4;丙:16;丁:7;戊:17.根据以上信息,下列判断正确的是
| A. |
戊同学手里拿的两张卡片上的数字是8和9 |
| B. |
丙同学手里拿的两张卡片上的数字是9和7 |
| C. |
丁同学手里拿的两张卡片上的数字是3和4 |
| D. |
甲同学手里拿的两张卡片上的数字是2和9 |
《西游记》、《三国演义》、《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著,某兴趣小组阅读四大名著的人数,同时满足以下三个条件:
(1)阅读过《西游记》的人数多于阅读过《水浒传》的人数;
(2)阅读过《水浒传》的人数多于阅读过《三国演义》的人数;
(3)阅读过《三国演义》的人数的2倍多于阅读过《西游记》的人数.
若阅读过《三国演义》的人数为4,则阅读过《水浒传》的人数的最大值为 .
某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分,某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是
A.甲B.甲与丁C.丙D.丙与丁
一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中 个小矩形的周长,就一定能算出这个大矩形的面积,则 的最小值是
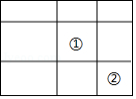
A.3B.4C.5D.6
为了从2018枚外形相同的金蛋中找出唯一的有奖金蛋,检查员将这些金蛋按 的顺序进行标号.第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,他将剩下的金蛋在原来的位置上又按 编了号(即原来的2号变为1号,原来的4号变为2号 原来的2018号变为1009号),又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋 如此下去,检查到最后一枚金蛋才是有奖金蛋,问这枚有奖金蛋最初的编号是 .
甲、乙、丙、丁4人进行乒乓球单循环比赛(每两个人都要比赛一场),结果甲胜了丁,并且甲、乙、丙胜的场数相同,则丁胜的场数是
A.3B.2C.1D.0
一个整数的所有正约数之和可以按如下方法求得,如:
,则6的所有正约数之和 ;
,则12的所有正约数之和 ;
,则36的所有正约数之和
.
参照上述方法,那么200的所有正约数之和为
A.420B.434C.450D.465
字母
,
,
,
各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形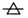 的连接方式为 .
的连接方式为 .
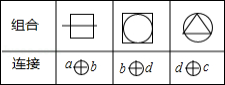
字母
,
,
,
各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形 的连接方式为 .
的连接方式为 .

"书法艺术课"开课后,某同学买了一包纸练习软笔书法,且每逢星期几写几张,即每星期一写1张,每星期二写2张, ,每星期日写7张,若该同学从某年的5月1日开始练习,到5月30日练习完后累积写完的宣纸总数超过120张,则可算得5月1日到5月28日他共用宣纸张数为 ,并可推断出5月30日应该是星期几 .
砸“金蛋”游戏:把210个“金蛋”连续编号为1,2,3, ,210,接着把编号是3的整数倍的“金蛋”全部砸碎;然后将剩下的“金蛋”重新连续编号为1,2,3, ,接着把编号是3的整数倍的“金蛋”全部砸碎 按照这样的方法操作,直到无编号是3的整数倍的“金蛋”为止.操作过程中砸碎编号是“66”的“金蛋”共 个.
如图是某剧场第一排座位分布图.甲、乙、丙、丁四人购票,所购票数分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位号之和最小,如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买1,2号座位的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一个购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序 .
