如图所示的防空导弹驱逐舰被誉为“中华神盾”。它满载时总重约为6×107N,驱逐舰满载以36km/h的速度匀速直线航行时,受到的阻力是总重的0.01倍,如果以这个速度匀速航行10h消耗燃油12t,问:
(1)驱逐舰航行时的牵引力是多大?
(2)航行时驱逐舰克服阻力做了多少功?
(3)整个航行过程中驱逐舰的效率是多大?(取q燃油=4×107J/kg)
阅读了教材“自制密度计”的课外小实验后,小叶和小王决定进行一下尝试.
(1)两人选择了一个由某种特殊材料制成的条形长方体A来制作密度计.小王测得A的质量为12g.当它漂浮在不同液面上时,所受到的浮力为 N.(g=10N/kg)
(2)小叶查阅了相关资料,在得知该材料的密度后,作出了如图甲所示的ρ﹣V图象,据图象可以找到关于A的一些信息.两人发现A的质量可以在ρ﹣V图中用阴影部分面积表示出来,请你在图中用斜线画出这一阴影部分.
(3)小王想用理论推导的方法,在A上标注出各种密度值.他选择首先标注水的密度,在测量出A的长度为20cm后,作出了图乙所示的示意图.经过计算,他确定出水面位置在距A上表面h= cm处,并作了标记.(ρ水=1.0×103kg/m3)•
(4)为了保证收益结果,两人将A放入足够多的水中,发现它不容易竖直漂浮.小叶在A的下端密绕了适量的金属丝(金属丝体积忽略不计),制成了“密度计”B.小王提醒他,如果这样,B的刻度应该与A不同.为了重新标注,他们应该测量的一个物理量是 .
(5)按照上述方法,两人在B上标注出了水、酒精、汽油等液体对应的刻度值,一个简易的密度计就制成了.
6月1日晚,“东方之星”客船翻沉事件不幸发生后,岳阳迅速行动,多部门积极参与搜援。参与搜救的某型号冲锋舟质量为180kg。
(1)求该冲锋舟受到的重力大小;
(2)该冲锋舟在水平地面时,与地面的接触面积为2m2,求它对水平地面的压强;
(3)该冲锋舟的排水量是1.2t,表示它满载时冲锋舟排开水的质量是1.2×103kg,求该冲锋舟满载时受到的浮力大小。
我国资源勘探返回式卫星是一个边长为1m的封闭式正方体,其总质量为2.0×103㎏.回收时,该卫星落回10m深的预定水域底部水平位置,假设用如图所示的打捞船上的装置匀速吊起,从卫星的上表面露出水面到下表面刚好离开水面的过程中,卫星受到的浮力是变化的,我们可以用一个恒力来代替,这个恒力的大小等于卫星受到的最大浮力的1/2,不计绳重和绳在水中受到的浮力,以及绳与滑轮间的摩擦.求: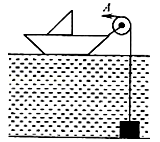
(1)起吊之前,卫星上表面受到水的压强;
(2)将卫星匀速吊起后在上表面未露出水面之前,作用在钢绳上A点的水平拉力;
(3)将卫星从水底打捞至下表面刚好离开水面的过程中,作用在A点的水平拉力做了多少功?
一个不规则的实心物体,质量55g,放入装满纯水的烧杯中,沉入底部,排开0.5N的水.然后向烧杯中加盐并搅拌,直到物体悬浮为止.(g=10N/kg)求:
(1)物体在纯水中所受的浮力;
(2)物体的体积;
(3)物体悬浮时盐水的密度.
某同学用圆柱形容器制作了一个测量物体质量的装置,它的底部较重,可以竖直漂浮在水面,总质量为0.21kg、底面积为3×10-3m2。不放物体时,在与水面所对应位置处标为质量的“0”刻度线,如图甲。求:(g取l0N/kg)
(1)不放物体时,该装置所受的浮力是多大?
(2)如图乙所示,在该装置中放入一个体积为1.5×10-5m3的物块A,装置底部在水面下的深度h=0.11m。此时与水面所对应位置处的刻度线应标为多少?
(3)物块A的密度是多少?
一个不规则的实心物体,质量55g,放入装满纯水的烧杯中,沉入底部,排开0.5N的水。然后向烧杯中加盐并搅拌,直到物体悬浮为止。
求:
(1)物体在纯水中所受的浮力;
(2)物体悬浮时盐水的密度。
一个底面积为10m2的圆柱状容器,装有适量的水,现在将一个体积为20m3、密度为0.8×103kg/m3的物体A放入其中,最终物体A漂浮于水面上.则:
(1)物体A所受到的浮力是多少?
(2)如图所示,若将画斜线部分截取下来并取出(其体积为浸入水中体积的一半),则取出的那部分物体的质量是多少?
(3)待剩余部分再次静止后,容器底部受到压强减小了多少?(g=10N/kg)
自制潜水艇模型如图所示,A为厚壁玻璃广口瓶,瓶的容积是V0,B为软木塞,C为排水管,D为进气细管,正为圆柱形盛水容器.当
瓶中空气的体积为V1时,潜水艇模型可以停在液面下任何深处,若通过细管D向瓶中压入空气,潜水艇模型上浮,当瓶中空气的体积为2 Vl时,潜水艇模型恰好有一半的体积露出水面,水的密度为恰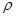 水 ,软木塞B,细管C、D的体积和重以及瓶中的空气重都不计.
水 ,软木塞B,细管C、D的体积和重以及瓶中的空气重都不计.
求:(1)潜水艇模型的体积;
(2)广口瓶玻璃的密度.
如图(a),在天平左盘放一杯水,右盘放砝码,使天平平衡.

(a) (b)
(1)将一质量为27g的铝块( 铝=2.7g/m3)放入左盘水中,水不溢出,天平还能平衡吗?
铝=2.7g/m3)放入左盘水中,水不溢出,天平还能平衡吗?
(2)将铝块如图(b)方式放入左盘中,天平还能平衡吗?
在水平桌面上竖直放置一个底面积为S的圆柱形容器,内装密度为 1的液体.将挂在弹簧测力计下体积为V的金属浸没在该液体中(液体未溢出).物体静止时,弹簧测力计示数为F;撤去弹簧测力计,球下沉并静止于容器底部,此时液体对容器底的压力为容器底对金属球的支持力的n倍.
1的液体.将挂在弹簧测力计下体积为V的金属浸没在该液体中(液体未溢出).物体静止时,弹簧测力计示数为F;撤去弹簧测力计,球下沉并静止于容器底部,此时液体对容器底的压力为容器底对金属球的支持力的n倍.
求(1)金属球的密度;(2)圆柱形容器内液体的质量.
底面积为400cm2的圆柱形容器内装有适量的水,将其竖直放在水平桌面上,把边长为10cm的正方体木块A放入水后,再在木块A的上方放一物体B,物体B恰好没入水中,如图1—5—11(a)所示.已知物体B的密度为6×103kg/m3.质量为0.6kg.(取g=10N/kg)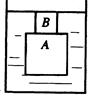
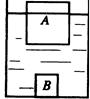
(a) (b)
求:(1)木块A的密度.
(2)若将B放入水中,如图(b)所示,求水对容器底部压强的变化.
如图所示的木块浸没在水中,细线对木块的拉力是2N.剪断细线,待木块静止后,将木块露出水面的部分切去,再在剩余的木块上加1N向下的压力时,木块有20cm3的体积露出水面.求木块的密度.(g取10N/kg) 
如图所示,一个木块用细绳系在容器的底部,向容器内倒水,当木块露出水面的体积是20cm3,时,细绳对木块的拉力为0.6N.将细绳剪断,木块上浮,静止时有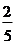 的体积露出水面,如图(b)所示,求此时木块受到的浮力.(g取10N/kg)
的体积露出水面,如图(b)所示,求此时木块受到的浮力.(g取10N/kg)
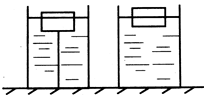
(a) (b)