有若干人去打猎,平均6人猎得5只野兔,15人猎得2只鹿,10人猎得1只野猪,结果最后每人分得一只猎物还多 4 只,问参加打猎的人数是多少?
有若干学生参加数学竞赛,每个学生的得分都是整数。已知参赛学生所得的总分是4729分,并且前三名的分数分别是88分、85分、80分,最低分是30分;又知道没有与前三名得分相同的学生,其他同学得分相同的人数都不超过3人。那么在这次竞赛中得分不低于60分的学生至少有多少人?
妈妈买来一篮橘子分给全家人,如果其中两人分4个,其余人每人分2个,则多出4个;如果其中一人分6个,其余人每人分4个,则缺少12个,妈妈买来橘子多少个?全家共有多少人?
我们的教室长12米,宽8米,高4米,粉刷其屋顶及四面墙壁,每平方米用涂料1.5千克,扣除门窗面积 22平方米,考虑到实际粉刷时有浪费,备料时增加所需涂料的 ,粉刷这间教室要准备多少千克的涂料?
,粉刷这间教室要准备多少千克的涂料?
购物.
| 品名 |
上衣 |
裤子 |
裙子 |
| 原价 |
60元 |
||
| 折扣 |
七折 |
八折 |
七折 |
| 现价 |
54元 |
(1)先将表中关于上衣和裤子表中服装的价格填写完整.
(2)妈妈记得裤子打八折时比原价便宜了6元,请你算一算,打八折后的价钱.并完成表格.
(3)妈妈按现价给芳芳买了一件上衣和一条裙子,正好花了她所带钱数的 .妈妈带了多少钱?
.妈妈带了多少钱?
请在下面直线上任意取一点O,并以O点为圆心画一个直径为4厘米的圆.在圆上挖取一个最大的正方形.(剩下的用阴影表示)计算这个阴影部分的面积.
.
如下图,ABCD是一个边长为6米的正方形模拟跑道,甲玩具车从A出发顺时针行进,速度是每秒5厘米,同时乙玩具车从CD的中点E处出发逆时针行进,结果两车第二次相遇恰好是在B点,求乙车每秒走多少厘米?
电车公司维修站有7辆电车需要维修.如果用一名工人维修这7辆电车的修复时间分别为12,17,8,18,23,30,14分钟.每辆电车每停开1分钟的经济损失是11元.现在由3名工作效率相同的维修工人各自单独工作,要使经济损失减到最小程度,那么最小的损失是多少元?
一条单线铁路线上有A,B,C,D,E五个车站,它们之间的路程如下图所示(单位:千米).两列火车从A,E相向对开,A车先开了3分钟,每小时行60千米,E车每小时行50千米,两车在车站上才能停车,互相让道、错车.两车应该安排在哪一个车站会车(相遇),才能使停车等候的时间最短,先到的火车至少要停车多长时间?
为了贯彻落实市委市府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A、B两贫困村的计划.现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表: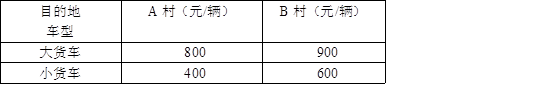
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若AB=4,求FH的长(结果保留根号).
学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下: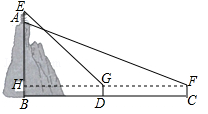
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.( 取1.732,结果保留整数)
取1.732,结果保留整数)
已知,在矩形ABCD中,E为BC边上一点,AE⊥DE,AB=12,BE=16,F为线段BE上一点,EF=7,连接AF.如图①,现有一张硬质纸片△GMN,∠NGM=90°,NG=6,MG=8,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上.如图②,△GMN从图①的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点出发,以每秒1个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ.当点N到达终点B时,△GMN和点P同时停止运动.设运动时间为t秒,解答下列问题:
(1)在整个运动过程中,当点G在线段AE上时,求t的值.
(2)在整个运动过程中,是否存在点P,使△APQ是等腰三角形.若存在,求出t的值;若不存在,说明理由.
(3)在整个运动过程中,设△GMN与△AEF重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.