在平面直角坐标系中,已知A(1,1),要在坐标轴上找一点P,使得△PAO为等腰三角形,这样的P点有几个()
| A.9 | B.8 | C.7 | D.6 |
如图,等边三角形OAB的一边OA在x轴上,双曲线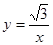
 在第一象限内的图像经过OB边的中点C,则点B的坐标是()
在第一象限内的图像经过OB边的中点C,则点B的坐标是()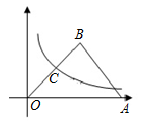
A.( 1,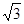 ) ) |
B.(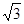 ,1 ) ,1 ) |
C.( 2,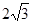 ) ) |
D.(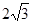 ,2 ) ,2 ) |
如图,是一组按照某种规律摆放而成的图案,第1个图有1个三角形,第二个图有4个三角形,第三个图有8个三角形,第四个图有12个三角形,则图5中三角形的个数是()
| A.8 | B.12 | C.16 | D.17 |
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是()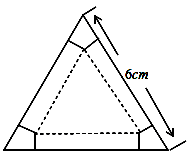
A.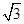 cm2 cm2 |
B. cm2 cm2 |
C.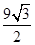 cm2 cm2 |
D.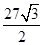 cm2 cm2 |
在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为().
A.22 B.24 C.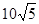 D.
D.
已知n是正整数,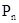 (
(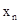 ,
,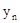 )是反比例函数
)是反比例函数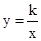 图象上的一列点,其中
图象上的一列点,其中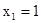 ,
,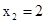 ,…,
,…,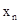 =n; 记
=n; 记 ,
,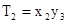 ,…,
,…,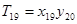 ;若
;若 ,则
,则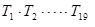 的值是()
的值是()
| A.0.1×218 | B.0.1×219 |
| C.0.1×220 | D.0.1×221 |
根据下列表格的对应值:
判断方程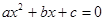 (
(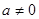 ,
,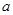 、
、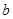 、
、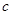 为常数)一个解的范围是()
为常数)一个解的范围是()
| A.3<x<3.23 | B.3.23<x<3.24 |
| C.3.24<x<3.25 | D.3.25<x<3.26 |
若函数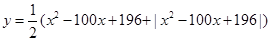 ,则当自变量
,则当自变量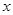 取1、2、3、…、100这100个自然数时,函数值的和是()。
取1、2、3、…、100这100个自然数时,函数值的和是()。
| A.540 | B.390 | C.194 | D.97 |
如图,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中 ,
, ,
, ,…的圆心依次按A,B,C循环.如果AC=1,那么曲线CDEF和线段CF围成图形的面积为( )
,…的圆心依次按A,B,C循环.如果AC=1,那么曲线CDEF和线段CF围成图形的面积为( )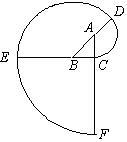
A.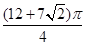 |
B. |
C.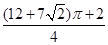 |
D.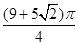 |
如图,数轴上的A、B、C、D四点所表示的数分别为a、b、c、d,且O为原点.根据图中各点位置,判断|a-c|之值与下列选项中哪个不同()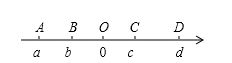
A.|a-b|+|c-b| B.|a|+|d|-|c+d|
C.|a-d|-|d-c| D.|a|+|d|-|c-d|
将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形,且它的一条直角边等于斜边的一半.图①~④中这样的图形有()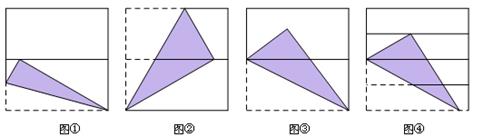
| A.4个 | B.3个 | C.2个 | D.1个 |
对于每个非零自然数n,抛物线 与x轴交于An、Bn两点,以
与x轴交于An、Bn两点,以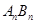 表示这两点间的距离,则
表示这两点间的距离,则 的值是( )
的值是( )
A.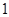 |
B.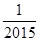 |
C.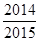 |
D.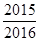 |
如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆, 则第8个图形中花盆的个数为()
则第8个图形中花盆的个数为()
| A.56 | B.64 | C.72 | D.90 |
如图,直线x=t(t>0)与反比例函数y=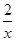 ,y=
,y=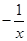 的图象分别交于B,C两点,A为y轴上的任意一点,则△ABC的面积为()
的图象分别交于B,C两点,A为y轴上的任意一点,则△ABC的面积为()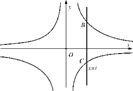
| A.3 | B.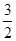 t t |
C.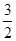 |
D.不能确定 |