初中数学三角形的五心试题

如图，在△ABC中，D是BC延长线上一点，∠B=40°，∠ACD=120°，则∠A等于（  ）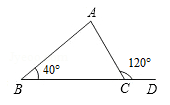

A．60°

B．70°

C．80°

D．90°

下列长度的四根木棒中，能与长为4cm，9cm的两根木棒围成一个三角形的是(    )

A．4cm

B．5cm

C．9cm

D．14cm

如图所示的图形中，若去掉一个的角得到一个五边形，则     °．

如图，已知∠B=∠C，AD=AE，则AB=AC，请说明理由（填空）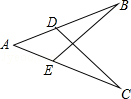

解：在△ABC和△ACD中，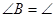
    （     ）
    （     ）
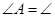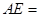       （已知）
∴△ABE≌△ACD （     ）
∴AB=AC（                      ）

在△ABC中，满足下列条件：①∠A=60°，∠C=30°；②∠A +∠B=∠C；③∠A：∠B：∠C=2:3:4； ④∠A=90°- ∠C，能确定△ABC是直角三角形的有（   ）

A．1个

B．2个

C．3个

D．4个

如图，已知∠BAC=∠DAE，AB=AD，下列条件无法确定△ABC≌△ADE的是（  ） 

A．∠E=∠C

B．BC=DE

C．AE=AC

D．∠B=∠D

一个多边形截去一个角后，形成另一个多边形的内角和为2520°，则原多边形的边数是（     ）

A．15或17

B．16或15

C．15

D．16或15或17

能将三角形面积平分的是三角形的（  ）

A．角平分线

B．高

C．中线

D．外角平分线

若一个正多边形的每个内角为140°，则这个多边形的边数为（   ）

A．9

B．8

C．7

D．6

已知三角形的两边长分别为4cm和9cm，则下列长度的四条线段中能作为第三边的是（    ） 

A．13cm

B．6cm

C．5cm

D．4cm

如果一个三角形两边为3cm，7cm，且第三边为奇数，则三角形的周长是_________．

已知一个n边形的内角和是其外角和的5倍，则n=__________．

如图所示，已知∠C=∠D=90°，AB=AE，增加下列一个条件（1）AC=AD，（2）BC=ED，（3）∠B=∠E，（4）∠1=∠2，其中能使△ABC≌△AED成立的条件有（ ）

A．4个

B．3个

C．2个

D．1个

如图，∠1=∠2，∠C=∠D，AC、BD交于E点，下列结论中不正确的是    （   ）

A．∠DAE=∠CBE   
B．ΔDEA不全等于ΔCEB
C．CE=DE          
D．ΔEAB是等腰三角形

如图，∠MON=90°，边长为4的等边三角形ABC的顶点A、B分别在边OM，ON上当B在边ON上运动时，A随之在边OM上运动，等边三角形的形状保持不变，运动过程中，点C到点O的最大距离为         ，